
已知双曲线C:![]() (a>0,b>0)的离心率
(a>0,b>0)的离心率![]() 为
为![]() ,右准线方程为
,右准线方程为![]() .
.
(Ⅰ)求![]() 双曲线C的方程;
双曲线C的方程;
(Ⅱ)设直线l是圆O:x2+y2=2上动点P(x0,y0)(x0y0≠0)处的切线,l与双曲线C交于不同的两点A,B,证明∠AOB的大小为定值.
分析:由![]() 以及
以及![]() 易求第(Ⅰ)问结论,
易求第(Ⅰ)问结论,
第(Ⅱ)问圆x2+y2=2![]() 上点P(x0,y0)处切线方程为x0x+y0y=2,代入椭圆中,利用根与系数的关系求解
上点P(x0,y0)处切线方程为x0x+y0y=2,代入椭圆中,利用根与系数的关系求解![]() =0即证.
=0即证.
解法一:(Ⅰ)由题意得
解得a=1,![]() .
.
所以b2=c2-a2=2.
所以双曲线C的方程为![]()
![]() .
.
(Ⅱ)点P(x0,y0)(x0y0≠0)在圆x2+y2=2上,
圆在点P(x0,y0)处的切线l的方程为![]() ,
,
化简得x0x+y0y=2.
由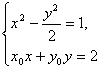 及x02+y02=2,得(3x02-4)x2-4x0x+8-2x02=0.
及x02+y02=2,得(3x02-4)x2-4x0x+8-2x02=0.
因为切线l与双曲线C交于不同的两点A,B且0<x02<2,
所以3x02-4≠0![]() ,且Δ=16x02-4(3x02-4)(8-2x02)>0.
,且Δ=16x02-4(3x02-4)(8-2x02)>0.
设A,B两点的坐标分别为(x1,y1),(x2,y2),
则![]() ,
, .
.
因为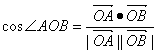 ,
,
且![]() =x1x2+y1y2=
=x1x2+y1y2=![]()
=![]()
=
= ,
,
所以∠AOB的大小为90°.
解法二:(Ⅰ)同解法一.
(Ⅱ)点P(x0,y0)(x0y0≠0)在圆x2+y2=2上,
圆在点P(x0,y0)处的切线l的方程为
![]() ,
,
化简得x0x+y0y=2.
由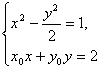 及x02+y02=2,得
及x02+y02=2,得
(3x02-4)x2-4x0x+8-2x02=0,①
(3x02-4)y2+8y0y-8+2x02=0.②
因为切线l与双曲线C交于不同的两点A,B,所以3x02-4≠0.
设A,B两点的坐标分别为(x1,y1),(x2,y2),
则 ,
,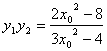 .所以
.所以![]() =x1x2+y1y2=0.
=x1x2+y1y2=0.
所以∠AOB的大小为90°.
(因为x02+y02=2且x0y0≠0,所以0<x02<2,0<y02<2,从而当3x02-4≠0时,方程①与方程②的判别式均大于0)


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
2
| ||
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
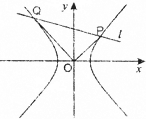 已知双曲线C:
已知双曲线C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 5 |
| 3 |
| OP |
| OQ |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省绵阳市高三第三次诊断性考试理科数学试卷(解析版) 题型:选择题
已知双曲线C: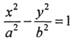 (a>09 b>0)的右焦点为F,过F且斜率为
(a>09 b>0)的右焦点为F,过F且斜率为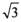 的直线交C于A,B两点,若
的直线交C于A,B两点,若 ,则C的离心率为
,则C的离心率为
(A)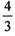 (B)
(B)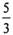 (C) 2
(D)
(C) 2
(D)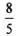
查看答案和解析>>
科目:高中数学 来源:2010-2011学年四川省南充市高三第二次诊断性考试理科数学卷 题型:选择题
已知双曲线C: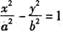 (a>0,b>0)的右焦点为F,过F且斜率为
(a>0,b>0)的右焦点为F,过F且斜率为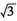 的直线交C于A、B两点,若
的直线交C于A、B两点,若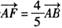 ,则C的离心率为( )
,则C的离心率为( )
A.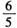 B.
B.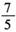 C.
C.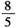 D.
D.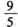
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com