
分析 根据终边相同的角相差360°的整数倍,利用集合的描述法可写出符合条件的集合,进行求解即可.
解答 解:根据终边相同的角相差360°的整数倍,
(1)-210°;
故与-210°终边相同的角可表示为:{α|α=k•360°-210°,k∈Z}.
则当k=0时,α=0×360°-210°=-210°,此时为最大的负角.
当k=1时,α=1×360°-210°=150°,此时为最小的正角.
(2)-1484°37′.
故与-1484°37′终边相同的角可表示为:{α|α=k•360°-1484°37′,k∈Z}.
则当k=4时,α=4×360°-1484°37′=-44°37′,此时为最大的负角.
当k=5时,α=5×360°-1484°37′=315°23′,此时为最小的正角.
点评 本题主要考查终边相同的角的集合,注意集合的表示方法是解题的关键,属基础题.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
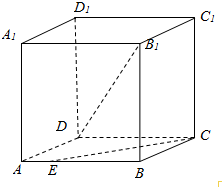 如图,正方体ABCD-A1B1C1D1的棱长为1,点E在棱AB上,且AE=m.已知异面直线DB1与CE所成角的余弦值等于$\frac{{\sqrt{3}}}{15}$,求m的值.
如图,正方体ABCD-A1B1C1D1的棱长为1,点E在棱AB上,且AE=m.已知异面直线DB1与CE所成角的余弦值等于$\frac{{\sqrt{3}}}{15}$,求m的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com