
【题目】在直角坐标系xOy中,曲线C1的参数方程为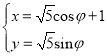 (φ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(φ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系.
(1)求C1的极坐标方程;
(2)若C1与曲线C2:ρ=2sinθ交于A,B两点,求|OA||OB|的值.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】椭圆![]() :
:![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 的面积为1,
的面积为1,![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上一点,
上一点,![]() 、
、![]() 是椭圆的左右两个焦点,直线
是椭圆的左右两个焦点,直线![]() 、
、![]() 分别交
分别交![]() 于
于![]() 、
、![]() ,是否存在点
,是否存在点![]() ,使
,使![]() ,若存在,求出
,若存在,求出![]() 点的横坐标;若不存在,请说明理由.
点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华为手机作为全球手机销量第二位,一直深受消费者喜欢.据调查数据显示,2019年度华为手机(含荣耀)在中国市场占有率接近![]() !小明为了考查购买新手机时选择华为是否与年龄有一定关系,于是随机调查100个2019年购买新手机的人,得到如下不完整的列表.定义30岁以下为“年轻用户”,30岁以上为“非年轻用户”.
!小明为了考查购买新手机时选择华为是否与年龄有一定关系,于是随机调查100个2019年购买新手机的人,得到如下不完整的列表.定义30岁以下为“年轻用户”,30岁以上为“非年轻用户”.
购买华为 | 购买其他 | 总计 | |
年轻用户 | 28 | ||
非年轻用户 | 24 | 60 | |
总计 |
附: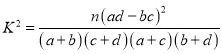 .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
(1)将列表填充完整,并判断是否有![]() 的把握认为购买手机时选择华为与年龄有关?
的把握认为购买手机时选择华为与年龄有关?
(2)若采用分层抽样的方法从购买华为手机用户中抽出6个人,再随机抽2人,求恰好抽到的两人都是非年轻用户的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二面角P﹣AB﹣C的大小为120°,且∠PAB=∠ABC=90°,AB=AP,AB+BC=6.若点P,A,B,C都在同一个球面上,则该球的表面积的最小值为( )
A.45πB.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“割圆术”是刘徽最突出的数学成就之一,他在《九章算术注》中提出割圆术,并作为计算圆的周长,面积已经圆周率的基础,刘徽把圆内接正多边形的面积一直算到了正3072边形,并由此而求得了圆周率为3.1415和3.1416这两个近似数值,这个结果是当时世界上圆周率计算的最精确数据.如图,当分割到圆内接正六边形时,某同学利用计算机随机模拟法向圆内随机投掷点,计算得出该点落在正六边形内的频率为0.8269,那么通过该实验计算出来的圆周率近似值为(参考数据:![]() )
)

A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() (
(![]() 为自然对数的底数,
为自然对数的底数,![]() ).
).
(1)当![]() 时,求函数
时,求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在区间
在区间![]() 上具有单调性,求
上具有单调性,求![]() 的取值范围;
的取值范围;
(3)若函数![]()
![]() 有且仅有
有且仅有![]() 个不同的零点
个不同的零点![]() ,且
,且![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】各项均为非负整数的数列{an}同时满足下列条件:
①a1=m(m![]() N*);②ann-1(n≥2);③n是a1+a2+‥+an的因数(n ≥1).
N*);②ann-1(n≥2);③n是a1+a2+‥+an的因数(n ≥1).
(Ⅰ)当m=5时,写出数列{an}的前五项;
(Ⅱ)若数列{an}的前三项互不相等,且n≥3时,an为常数,求m的值;
(Ⅲ)求证:对任意正整数m,存在正整数M,使得n≥M时,an为常数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com