
【题目】若方程|x2﹣2x﹣1|﹣t=0有四个不同的实数根x1、x2、x3、x4,且x1<x2<x3<x4 , 则2(x4﹣x1)+(x3﹣x2)的取值范围是( )
A.(8,6 ![]() )
)
B.(6 ![]() ,4
,4 ![]() )
)
C.[8,4 ![]() ]
]
D.(8,4 ![]() ]
]
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC=![]() AD,∠BAD=∠ABC=90°,E是PD的中点.
AD,∠BAD=∠ABC=90°,E是PD的中点.
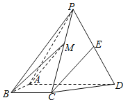
(1)证明:直线CE∥平面PAB;
(2)点M在棱PC上,且直线BM与底面ABCD所成角为45°,求二面角M-AB-D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:极坐标与参数方程]
在直角坐标系xOy中,直线l的参数方程为 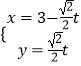 (t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位),且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4sinθ.
(t为参数).在极坐标系(与直角坐标系xOy取相同的长度单位),且以原点O为极点,以x轴正半轴为极轴)中,圆C的方程为ρ=4sinθ.
(1)求圆C的直角坐标方程和直线l普通方程;
(2)设圆C与直线l交于点A,B,若点P的坐标为(3,0),求|PA|+|PB|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,且2cosAcosC(tanAtanC﹣1)=1.
(Ⅰ)求B的大小;
(Ⅱ)若 ![]() ,
, ![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人进行某项对抗性游戏,采用“七局四胜”制,即先赢四局者为胜,若甲、乙两人水平相当,且已知甲先赢了前两局.
![]() Ⅰ
Ⅰ![]() 求乙取胜的概率;
求乙取胜的概率;
![]() Ⅱ
Ⅱ![]() 记比赛局数为X,求X的分布列及数学期望
记比赛局数为X,求X的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校青年职工、中年职工、老年职工的人数之比为7:5:3,为了了解该单位职工的健康情况,用分层抽样的方法从中抽取样本 .若样本中的青年职工为14人,则样本容量为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+2﹣x .
(1)求方程f(x)= ![]() 的根;
的根;
(2)求证:f(x)在[0,+∞)上是增函数;
(3)若对于任意x∈[0,+∞),不等式f(2x)≥f(x)﹣m恒成立,求实数m的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com