
或

分析:分0<a<1和a>1时两种情况加以讨论,根据指数函数的单调性和一次函数单调性,并结合分段函数在区间端点处函数值的大小比较,求出函数在[0,2]上的最大值和最小值,由此根据题意建立关于a的方程,解之即得满足条件的实数a的值.
解答:①当0<a<1时,可得
在[0,1]上,f(x)=a
x是减函数;且在(1,2]上,f(x)=-x+a是减函数
∵f(0)=a
0=1>-1+a,∴函数的最大值为f(0)=1;
而f(2)=-2+a<a=f(1),所以函数的最小值为f(2)=-2+a
因此,-2+a+

=1,解之得a=

∈(0,1)符合题意;
②当a>1时,可得
在[0,1]上,f(x)=a
x是增函数;且在(1,2]上,f(x)=-x+a是减函数
∵f(1)=a>-1+a,∴函数的最大值为f(1)=a
而f(2)=-2+a,f(0)=a
0=1,可得
i)当a∈(1,3]时,-2+a<1,得f(2)=-2+a为函数的最小值,
因此,-2+a+

=a矛盾,找不出a的值.
ii)当a∈(3,+∞)时,-2+a>1,得f(0)=1为函数的最小值,
因此,1+

=a,解之得a=

∈(3,+∞),符合题意.
综上所述,实数a的值为

或

故答案为:

或

点评:本题给出含有字母a的分段函数,在已知函数的最大最小值之差的情况下求参数a的值,着重考查了指数函数、一次函数的单调性和分段函数的理解等知识,考查了转化化归和分类讨论的数学思想,属于中档题.

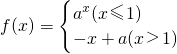 若函数f(x)在[0,2]上的最大值比最小值大
若函数f(x)在[0,2]上的最大值比最小值大 ,则a的值为________.
,则a的值为________. 或
或
 =1,解之得a=
=1,解之得a= ∈(0,1)符合题意;
∈(0,1)符合题意; =a矛盾,找不出a的值.
=a矛盾,找不出a的值. =a,解之得a=
=a,解之得a= ∈(3,+∞),符合题意.
∈(3,+∞),符合题意. 或
或
 或
或


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案