
【题目】某P2P平台需要了解该平台投资者的大致年龄分布,发现其投资者年龄大多集中在区间![]() 岁之间,对区间
岁之间,对区间![]() 岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:
岁的人群随机抽取20人进行了一次理财习惯调查,得到如下统计表和各年龄段人数频率分布直方图:

组数 | 分组 | 人数 |
第一组 |
| 2 |
第二组 |
| a |
第三组 |
| 5 |
第四组 |
| 4 |
第五组 |
| 3 |
第六组 |
| 2 |
(1)求a的值并画出频率分布直方图;
(2)从被调查的20人且年龄在![]() 岁中的投资者中随机抽取3人调查对其P2P理财观的看法活动,记这3人中来自于区间
岁中的投资者中随机抽取3人调查对其P2P理财观的看法活动,记这3人中来自于区间![]() 岁年龄段的人数为X,求随机变量X的分布列及数学期望.
岁年龄段的人数为X,求随机变量X的分布列及数学期望.
 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】近年来,我国电子商务行业迎来了蓬勃发展的新机遇,但是电子商务行业由于缺乏监管,服务质量有待提高.某部门为了对本地的电商行业进行有效监管,调查了甲、乙两家电商的某种同类产品连续十天的销售额(单位:万元),得到如下茎叶图:
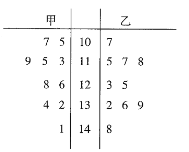
(1)根据茎叶图判断甲、乙两家电商对这种产品的销售谁更稳定些?
(2)如果日销售额超过平均销售额,相应的电商即被评为优,根据统计数据估计两家电商一个月(按30天计算)被评为优的天数各是多少.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.在做回归分析时,残差图中残差点分布的带状区域的宽度越窄表示回归效果越差
B.某地气象局预报:6月9日本地降水概率为90%,结果这天没下雨,这表明天气预报并不科学
C.回归分析模型中,残差平方和越小,说明模型的拟合效果越好
D.在回归直线方程![]() 中,当解释变量每增加1个单位时,预报变量多增加0.1个单位
中,当解释变量每增加1个单位时,预报变量多增加0.1个单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社会机构为了调查对手机游戏的兴趣与年龄的关系,通过问卷调查,整理数据得如下![]() 列联表:
列联表:
40岁以下 | 40岁以上 | 合计 | |
很兴趣 | 30 | 15 | 45 |
无兴趣 | 20 | 35 | 55 |
合计 | 50 | 50 | 100 |
(1)根据列联表,能否有![]() 的把握认为对手机游戏的兴趣程度与年龄有关?
的把握认为对手机游戏的兴趣程度与年龄有关?
(2)若已经从![]() 岁以下的被调查者中用分层抽样的方式抽取了
岁以下的被调查者中用分层抽样的方式抽取了![]() 名,现从这
名,现从这![]() 名被调查者中随机选取
名被调查者中随机选取![]() 名,求这
名,求这![]() 名被调查者中恰有
名被调查者中恰有![]() 名对手机游戏无兴趣的概率.
名对手机游戏无兴趣的概率.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.84 | 6.635 | 10.828 |
(注:参考公式: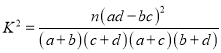 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就.在“杨辉三角”中,第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列
,若去除所有为1的项,依次构成数列![]() ,则此数列的前55项和为( )
,则此数列的前55项和为( )

A. 4072B. 2026C. 4096D. 2048
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随机调查某城市80名有子女在读小学的成年人,以研究晚上八点至十点时间段辅导子女作业与性别的关系,得到下面的数据表:
是否辅导 性别 | 辅导 | 不辅导 | 合计 |
男 | 25 | 60 | |
女 | |||
合计 | 40 | 80 |
(1)请将表中数据补充完整;
(2)用样本的频率估计总体的概率,估计这个城市有子女在读小学的成人女性晚上八点至十点辅导子女作业的概率;
(3)根据以上数据,能否有99%以上的把握认为“晚上八点至十点时间段是否辅导子女作业与性别有关?”.
参考公式: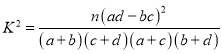 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() 离心率
离心率![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)经过椭圆左焦点![]() 的直线(不经过点
的直线(不经过点![]() 且不与
且不与![]() 轴重合)与椭圆交于
轴重合)与椭圆交于![]() 两点,与直线
两点,与直线![]() :
:![]() 交于点
交于点![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .则是否存在常数
.则是否存在常数![]() ,使得向量
,使得向量![]()
![]() 共线?若存在求出
共线?若存在求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com