
【题目】已知函数![]() 在
在![]() 处的切线方程为
处的切线方程为![]()
(1)若![]() =
= ![]() ,求证:曲线
,求证:曲线![]() 上的任意一点处的切线与直线
上的任意一点处的切线与直线![]() 和直线
和直线![]() 围成的三角形面积为定值;
围成的三角形面积为定值;
(2)若![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 对于定义域内的任意
对于定义域内的任意![]() 都成立;
都成立;
(3)在(2)的条件下,若方程![]() 有三个解,求实数
有三个解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)详见解析(2)![]()
【解析】试题分析:根据导数的几何意义, ![]() 为切线的斜率,解出
为切线的斜率,解出![]() ,写出
,写出![]() 的切线方程求出三角形的面积为定值.利用
的切线方程求出三角形的面积为定值.利用![]() 求出
求出![]() ,假设存在
,假设存在![]() 满足题意,则式子
满足题意,则式子![]() 对定义域任一
对定义域任一![]() 恒成立,解出
恒成立,解出![]() ;代入
;代入![]() 的值使方程
的值使方程![]() 有三个解,化为
有三个解,化为![]() ,画出
,画出![]() 的图象,要求
的图象,要求![]() <
<![]() <0,解出
<0,解出![]() 的范围.
的范围.
试题解析:(1)因为 f′(x)= ![]()
所以 f′(3)= ![]() ,
, ![]()
又 g(x)=f(x+1)=ax+![]() ,
,
设g(x)图象上任意一点P(x0,y0)因为 g′(x)=a﹣![]() ,
,
所以切线方程为y﹣(ax0+![]() )=(a﹣
)=(a﹣![]() )(x﹣x0)
)(x﹣x0)
令x=0 得y=![]() ; 再令y=ax得 x=2x0,
; 再令y=ax得 x=2x0,
故三角形面积S=![]() |
|![]() ||2x0|=4,
||2x0|=4,
即三角形面积为定值.
(2)由f(3)=3得a=1,f(x)=x+![]() ﹣1假设存在
﹣1假设存在![]() 满足题意,
满足题意,
则有x﹣1+![]() +m﹣x﹣1+
+m﹣x﹣1+![]() =k
=k
化简,得 ![]() 对定义域内任意x都成立,
对定义域内任意x都成立,
故只有![]() 解得
解得![]()
所以存在实数m=2,k=0使得f(x)+f(m﹣k)=k对定义域内的任意都成立.
(3)由题意知,x﹣1+![]() =t(x2﹣2x+3)|x|
=t(x2﹣2x+3)|x|
因为x≠0,且x≠1化简,得 t=![]()
即![]() =|x|(x﹣1),
=|x|(x﹣1),
如图可知,﹣![]() <
<![]() <0,
<0,
所以t<﹣4即为t的取值范围.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,有一块半圆形空地,开发商计划建一个矩形游泳池ABCD及其矩形附属设施EFGH,并将剩余空地进行绿化,园林局要求绿化面积应最大化.其中半圆的圆心为O,半径为R,矩形的一边AB在直径上,点C、D、G、H在圆周上,E、F在边CD上,且![]() ,设
,设![]()
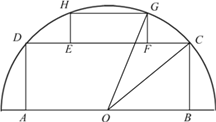
(1)记游泳池及其附属设施的占地面积为![]() ,求
,求![]() 的表达式;
的表达式;
(2)当![]() 为何值时,能符合园林局的要求?
为何值时,能符合园林局的要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() ,关于实数
,关于实数![]() 的不等式
的不等式![]() 的解集为
的解集为![]() .
.
(1)当![]() 时,解关于
时,解关于![]() 的不等式:
的不等式: ![]() ;
;
(2)是否存在实数![]() ,使得关于
,使得关于![]() 的函数
的函数![]() (
(![]() )的最小值为
)的最小值为![]() ?若存在,求实数
?若存在,求实数![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() 中,
中, ![]() 为坐标原点,曲线
为坐标原点,曲线![]() :
:  (
(![]() 为参数),在以平面直角坐标系的原点为极点,
为参数),在以平面直角坐标系的原点为极点, ![]() 轴的正半轴为极轴,有相同单位长度的极坐标系中,直线
轴的正半轴为极轴,有相同单位长度的极坐标系中,直线![]() :
: ![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求与直线![]() 平行且与曲线
平行且与曲线![]() 相切的直线的直角坐标方程。
相切的直线的直角坐标方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值;
的最大值;
(2)令![]() ,其图象上存在一点
,其图象上存在一点![]() ,使此处切线的斜率
,使此处切线的斜率![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)当![]() ,
, ![]() 时,方程
时,方程![]() 有唯一实数解,求正数
有唯一实数解,求正数![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com