
【题目】已知函数![]()
(1)讨论函数![]() 的单调性;
的单调性;
(2)若函数![]() 有两个极值点
有两个极值点![]() ,证明:
,证明:![]()
【答案】(1)见解析;(2)证明见解析.
【解析】
(1)首先对函数求导,根据韦达定理与判别式确定二次函数根的分布,然后根据函数值的正负确定函数的单调性;
(2)首先求出![]() ,然后在对求出的表达式进行切线缩放即可证明不等式.
,然后在对求出的表达式进行切线缩放即可证明不等式.
(1)由题知函数的定义域为![]() ,
,
有![]() ,
,
对![]() 有
有![]() ,
,
当![]() 时
时![]() ,有
,有![]() ,
,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时
时![]() ,
,![]() 有两个根
有两个根![]() ,
,![]() ,设
,设![]() ,
,
根据韦达定理有![]() ,
,![]() ,
,
当![]() 时,
时,
![]() 有两个正根
有两个正根![]() ,
,![]() ,
,
可知当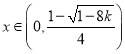 时
时![]() ,函数
,函数![]() 单调递增,
单调递增,
当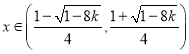 时
时![]() ,函数
,函数![]() 单调递减,
单调递减,
当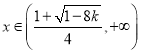 时
时![]() ,函数
,函数![]() 单调递增,
单调递增,
当![]() 时,
时,
![]() 有两个根
有两个根![]() ,
,![]() ,
,
可知当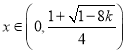 时
时![]() ,函数
,函数![]() 单调递减,
单调递减,
可知当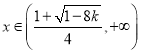 时
时![]() ,函数
,函数![]() 单调递增;
单调递增;
(2)由(1)知当![]() 时,函数有两个极值点
时,函数有两个极值点![]() ,
,![]() ,设
,设![]() ,
,
根据(1)中单调性可知函数![]() 在
在![]() 处取极大值,
处取极大值,![]() 处取极小值,
处取极小值,
所以![]() ,
,
代入![]() ,
,![]() ,
,
整理得![]() ,
,
令![]() ,有
,有![]() ,
,
有![]() ,
,
因为![]() ,
,
代入![]() 有
有![]() .
.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知平面直角坐标系![]() ,以
,以![]() 为极点,
为极点, ![]() 轴的非负半轴为极轴建立极坐标系,
轴的非负半轴为极轴建立极坐标系, ![]() 点的极坐标为
点的极坐标为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)写出点![]() 的直角坐标及曲线
的直角坐标及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 为曲线
为曲线![]() 上的动点,求
上的动点,求![]() 的中点
的中点![]() 到直线
到直线![]() :
: ![]() 的距离的最小值.
的距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某土特产超市为预估2020年元旦期间游客购买土特产的情况,对2019年元旦期间的90位游客购买情况进行统计,得到如下人数分布表.
购买金额(元) |
|
|
|
|
|
|
人数 | 10 | 15 | 20 | 15 | 20 | 10 |
(1)根据以上数据完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为购买金额是否少于60元与性别有关.
的把握认为购买金额是否少于60元与性别有关.
不少于60元 | 少于60元 | 合计 | |
男 | 40 | ||
18 | |||
合计 |
(2)为吸引游客,该超市推出一种优惠方案,购买金额不少于60元可抽奖3次,每次中奖概率为![]() (每次抽奖互不影响,且
(每次抽奖互不影响,且![]() 的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数
的值等于人数分布表中购买金额不少于60元的频率),中奖1次减5元,中奖2次减10元,中奖3次减15元.若游客甲计划购买80元的土特产,请列出实际付款数![]() (元)的分布列并求其数学期望.
(元)的分布列并求其数学期望.
附:参考公式和数据: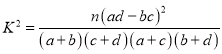 ,
,![]() .
.
附表:
| 2.072 | 2.706 | 3.841 | 6.635 | 7.879 |
| 0.150 | 0.100 | 0.050 | 0.010 | 0.005 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】1772年德国的天文学家波得发现了求太阳的行星距离的法则,记地球距离太阳的平均距离为10,可以算得当时已知的六大行星距离太阳的平均距离如下表:
星名 | 水星 | 金星 | 地球 | 火星 | 木星 | 土星 |
与太阳的距离 | 4 | 7 | 10 | 16 | 52 | 100 |
除水星外,其余各星与太阳的距离都满足波得定则(某一数列规律),当时德国数学家高斯根据此定则推算,火星和木星之间距离太阳28还有一颗大行星,1801年,意大利天文学家皮亚齐经过观测,果然找到了火星和木星之间距离太阳28的谷神星以及它所在的小行星带,请你根据这个定则,估算从水星开始由近到远算,第10个行星与太阳的平均距离大约是( )
A.388B.772C.1540D.3076
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,过点
,过点![]() 的直线交抛物线于
的直线交抛物线于![]() ,
,![]() 两点,点
两点,点![]() 在准线
在准线![]() 上的投影为
上的投影为![]() ,若
,若![]() 是抛物线上一点,且
是抛物线上一点,且![]() .
.
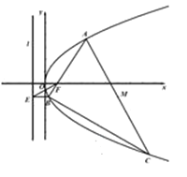
(1)证明:直线![]() 经过
经过![]() 的中点
的中点![]() ;
;
(2)求![]() 面积的最小值及此时直线
面积的最小值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的半径为2,
的半径为2,![]() 为平面上一点,
为平面上一点,![]() ,
,![]() 是圆上动点,线段
是圆上动点,线段![]() 的垂直平分线
的垂直平分线![]() 和直线
和直线![]() 相交于点
相交于点![]() .
.
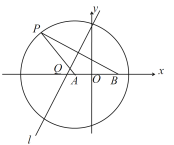
(1)以![]() 中点
中点![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,建立平面直角坐标系,求
轴,建立平面直角坐标系,求![]() 点的轨迹方程;
点的轨迹方程;
(2)设(1)中![]() 点轨迹与直线
点轨迹与直线![]() 相交于
相交于![]() 两点,求三角形
两点,求三角形![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通6座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,且保费与上一年度车辆发生道路交通事故的情况相联系.发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,且保费与上一年度车辆发生道路交通事故的情况相联系.发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
交强险浮动因素和费率浮动比率表 | ||
浮动因素 | 浮动比率 | |
| 上一个年度未发生有责任道路交通事故 | 下浮 |
| 上两个年度未发生有责任道路交通事故 | 下浮 |
| 上三个及以上年度未发生有责任道路交通事故 | 下浮 |
| 上一个年度发生一次有责任不涉及死亡的道路交通事故 |
|
| 上一个年度发生两次及两次以上有责任道路交通事故 | 上浮 |
| 上一个年度发生有责任道路交通死亡事故 | 上浮 |
某机构为了研究某一品牌普通6座以下私家车的投保情况,随机抽取了60辆车龄已满三年该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
(1)求一辆普通6座以下私家车在第四年续保时保费高于基本保费的频率;
(2)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车.假设购进一辆事故车亏损5000元,一辆非事故车盈利10000元.且各种投保类型车的频率与上述机构调查的频率一致,完成下列问题:
①若该销售商店内有6辆(车龄已满三年)该品牌二手车,某顾客欲在店内随机挑选2辆车,求这2辆车恰好有一辆为事故车的概率;
②若该销售商一次购进120辆(车龄已满三年)该品牌二手车,求一辆车盈利的平均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,如图,已知椭圆E:
中,如图,已知椭圆E:![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,上、下顶点分别为
,上、下顶点分别为![]() 、
、![]() .设直线
.设直线![]() 倾斜角的余弦值为
倾斜角的余弦值为![]() ,圆
,圆![]() 与以线段
与以线段![]() 为直径的圆关于直线
为直径的圆关于直线![]() 对称.
对称.

(1)求椭圆E的离心率;
(2)判断直线![]() 与圆
与圆![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)若圆![]() 的面积为
的面积为![]() ,求圆
,求圆![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com