
已知各项均为正数的两个无穷数列 、
、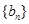 满足
满足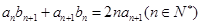 .
.
(Ⅰ)当数列 是常数列(各项都相等的数列),且
是常数列(各项都相等的数列),且 时,求数列
时,求数列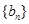 的通项公式;
的通项公式;
(Ⅱ)设 、
、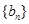 都是公差不为0的等差数列,求证:数列
都是公差不为0的等差数列,求证:数列 有无穷多个,而数列
有无穷多个,而数列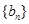 惟一确定;
惟一确定;
(Ⅲ)设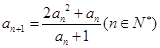 ,
,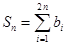 ,求证:
,求证: .
.
(Ⅰ)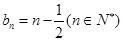 ;(Ⅱ)详见解析;(Ⅲ)详见解析.
;(Ⅱ)详见解析;(Ⅲ)详见解析.
【解析】
试题分析:(Ⅰ)由 是常数列,得
是常数列,得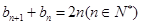 ,进而探求数列项间的关系;(Ⅱ)将等差数列
,进而探求数列项间的关系;(Ⅱ)将等差数列 、
、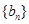 的通项公式代入
的通项公式代入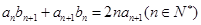 ,根据等式恒成立,求首项和公差;(Ⅲ)利用题中所给关系式对
,根据等式恒成立,求首项和公差;(Ⅲ)利用题中所给关系式对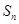 进行适当放缩,求出上界和下界.
进行适当放缩,求出上界和下界.
试题解析:
(Ⅰ)因为数列 是常数列,且
是常数列,且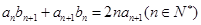 ,所以
,所以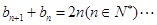 ①,因此
①,因此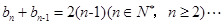 ②,①-②得,
②,①-②得,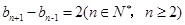 ,这说明数列
,这说明数列 的序号为奇数的项及序号为偶数的项均按原顺序组成公差为2的等差数列,又
的序号为奇数的项及序号为偶数的项均按原顺序组成公差为2的等差数列,又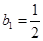 ,
,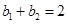 ,所以
,所以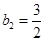 ,因此
,因此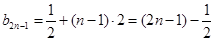 ,
,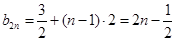 ,即
,即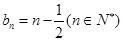 .
.
(Ⅱ)设 、
、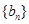 都是公差分别为
都是公差分别为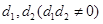 ,将其通项公式代入
,将其通项公式代入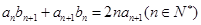 得
得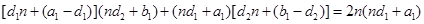 ,因为它是恒等式,所以
,因为它是恒等式,所以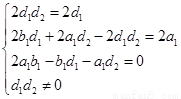 ,解得
,解得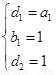 ,因此
,因此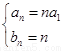 .
.
由于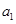 可以取无穷多非零的实数,故数列
可以取无穷多非零的实数,故数列 有无穷多个,而数列
有无穷多个,而数列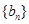 惟一确定;
惟一确定;
(Ⅲ)因为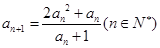 ,且
,且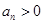 ,所以
,所以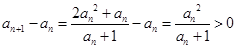 ,即
,即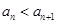 ,所以
,所以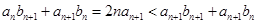 ,得
,得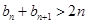 ,因此
,因此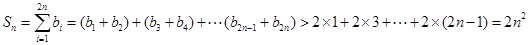 .
.
又由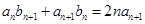 得,
得,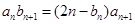 ,而
,而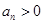 ,所以
,所以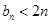 ,因此
,因此
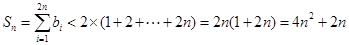 ,所以
,所以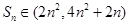 ,所以
,所以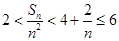 .
.
考点:等差数列、数列的递推关系、数列与不等式.


科目:高中数学 来源: 题型:
| n | 1 | 2 | 3 | 4 | 5 |
| an | 1 | 5 | 3 | 1 | 2 |
| bn | 1 | 6 | 2 | x | y |
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| ||
| 2 |
|
| bn |
| an |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+bn | ||||||
|
| bn |
| an |
| bn+1 |
| an+1 |
1+(
|
| bn |
| an |
| 2 |
| bn |
| an |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an+bn | ||
|
| bn |
| an |
| bn |
| an |
| 2 |
| bn |
| an |
查看答案和解析>>
科目:高中数学 来源: 题型:
定义数列{cn}:c1=0,cn=
|
n | 1 | 2 | 3 | 4 | 5 | |||||
| an | 1 | 5 | 3 | 1 | 2 | ||||||
| bn | 1 | 6 | 2 | x | y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com