
【题目】下面几种推理过程是演绎推理的是( )
A. 某校高三有8个班,1班有51人,2班有53人,3班有52人,由此推测各班人数都超过50人
B. 由三角形的性质,推测空间四面体的性质
C. 平行四边形的对角线互相平分,菱形是平行四边形,所以菱形的对角线互相平分
D. 在数列![]() 中,
中,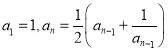 ,可得
,可得![]() ,由此归纳出
,由此归纳出![]() 的通项公式
的通项公式![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人独立地解决同一问题,甲解出此问题的概率是![]() ,乙解出此问题的概率是
,乙解出此问题的概率是![]() .求:
.求:
(1)甲、乙都解出此问题的概率;
(2)甲、乙都未解出此问题的概率;
(3)甲、乙恰有一人解出此问题的概率;
(4)至少有一人解出此问题的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】A,B两组各有7位病人,他们服用某种药物后的康复时间(单位:天)记录如下:
A组:10,11,12,13,14,15,16;
B组:12,13,15,16,17,14,![]() .
.
假设所有病人的康复时间相互独立,从A,B两组随机各选1人,A组选出的人记为甲,B组选出的人记为乙.
(1)求甲的康复时间不少于14天的概率;
(2)如果![]() ,求甲的康复时间比乙的康复时间长的概率.
,求甲的康复时间比乙的康复时间长的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某次测量中得到的A样本数据如下:52,54,54,56,56,56,55,55,55,55.若B样本数据恰好是A样本数据都加6后所得数据,则A,B两样本的下列数字特征对应相同的是( )
A. 众数 B. 平均数
C. 中位数 D. 标准差
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,在区间
,在区间![]() 上有最大值
上有最大值![]() ,最小值
,最小值![]() ,设函数
,设函数![]() .
.
(1)求![]() 的值;
的值;
(2)不等式![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)方程![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】质检部门从某超市销售的甲、乙两种食用油中分别随机抽取100桶检测某项质量指标,由检测结果得到如图的频率分布直方图:
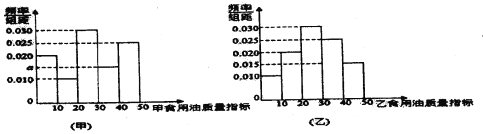
(I)写出频率分布直方图(甲)中![]() 的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为
的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为![]() ,试比较
,试比较![]() 的大小(只要求写出答案);
的大小(只要求写出答案);
(Ⅱ)佑计在甲、乙两种食用油中各随机抽取1桶,恰有一个桶的质量指标大于20,且另—个桶的质量指标不大于20的概率;
(Ⅲ)由频率分布直方图可以认为,乙种食用油的质量指标值![]() 服从正态分布
服从正态分布![]() .其中
.其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,设
,设![]() 表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55, 38.45)的桶数,求
表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55, 38.45)的桶数,求![]() 的数学期望.
的数学期望.
注:①同一组数据用该区间的中点值作代表,计算得![]() :
:
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].

(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.
分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
x∶y | 1∶1 | 2∶1 | 3∶4 | 4∶5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com