
【题目】已知函数![]() 只能同时满足下列三个条件中的两个:①函数
只能同时满足下列三个条件中的两个:①函数![]() 的最大值为2;②函数
的最大值为2;②函数![]() 的图象可由
的图象可由![]() 的图象平移得到;③函数
的图象平移得到;③函数![]() 图象的相邻两条对称轴之间的距离为
图象的相邻两条对称轴之间的距离为![]() .
.
(1)请写出这两个条件序号,并求出![]() 的解析式;
的解析式;
(2)求方程![]() 在区间
在区间![]() 上所有解的和.
上所有解的和.
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】若存在实常数![]() 和
和![]() ,使得函数
,使得函数![]() 和
和![]() 对其公共定义域上的任意实数x都满足:
对其公共定义域上的任意实数x都满足:![]() 和
和![]() 恒成立,则称此直线
恒成立,则称此直线![]() 为
为![]() 和
和![]() 的“隔离直线”,已知函数
的“隔离直线”,已知函数![]() ,
,![]() ,
,![]() (
(![]() 为自然对数的底数),则( )
为自然对数的底数),则( )
A.![]() 在
在![]() 内单调递增;
内单调递增;
B.![]() 和
和![]() 之间存在“隔离直线”,且
之间存在“隔离直线”,且![]() 的最小值为
的最小值为![]() ;
;
C.![]() 和
和![]() 之间存在“隔离直线”,且
之间存在“隔离直线”,且![]() 的取值范围是
的取值范围是![]() ;
;
D.![]() 和
和![]() 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线”![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 和圆
和圆![]() ,倾斜角为45°的直线
,倾斜角为45°的直线![]() 过抛物线
过抛物线![]() 的焦点,且
的焦点,且![]() 与圆
与圆![]() 相切.
相切.
(1)求![]() 的值;
的值;
(2)动点![]() 在抛物线
在抛物线![]() 的准线上,动点
的准线上,动点![]() 在
在![]() 上,若
上,若![]() 在
在![]() 点处的切线
点处的切线![]() 交
交![]() 轴于点
轴于点![]() ,设
,设![]() .求证点
.求证点![]() 在定直线上,并求该定直线的方程.
在定直线上,并求该定直线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点在
的焦点在![]() 轴上,中心在坐标原点,抛物线
轴上,中心在坐标原点,抛物线![]() 的焦点在
的焦点在![]() 轴上,顶点在坐标原点,在
轴上,顶点在坐标原点,在![]() 、
、![]() 上各取两个点,将其坐标记录于表格中:
上各取两个点,将其坐标记录于表格中:
|
|
|
|
|
|
|
|
|
|
(1)求![]() 、
、![]() 的标准方程;
的标准方程;
(2)已知定点![]() ,
,![]() 为抛物线
为抛物线![]() 上的一动点,过点
上的一动点,过点![]() 作抛物线
作抛物线![]() 的切线交椭圆
的切线交椭圆![]() 于
于![]() 、
、![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() 棱长为
棱长为![]() ,如图,
,如图,![]() 为
为![]() 上的动点,
上的动点,![]() 平面
平面![]() .下面说法正确的是( )
.下面说法正确的是( )
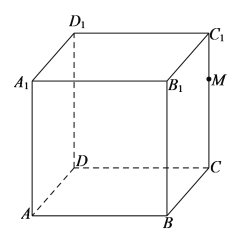
A.直线![]() 与平面
与平面![]() 所成角的正弦值范围为
所成角的正弦值范围为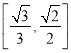
B.点![]() 与点
与点![]() 重合时,平面
重合时,平面![]() 截正方体所得的截面,其面积越大,周长就越大
截正方体所得的截面,其面积越大,周长就越大
C.点![]() 为
为![]() 的中点时,若平面
的中点时,若平面![]() 经过点
经过点![]() ,则平面
,则平面![]() 截正方体所得截面图形是等腰梯形
截正方体所得截面图形是等腰梯形
D.己知![]() 为
为![]() 中点,当
中点,当![]() 的和最小时,
的和最小时,![]() 为
为![]() 的中点
的中点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若曲线![]() 与曲线
与曲线![]() 在公共点处有共同的切线,求实数
在公共点处有共同的切线,求实数![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,试问函数![]() 是否有零点?如果有,求出该零点;若没有,请说明理由.
是否有零点?如果有,求出该零点;若没有,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着![]() 年北京冬奥会临近,中国冰雪产业快速发展,冰雪运动人数快速上升,冰雪运动市场需求得到释放,将引领户外用品行业市场增长.下面是
年北京冬奥会临近,中国冰雪产业快速发展,冰雪运动人数快速上升,冰雪运动市场需求得到释放,将引领户外用品行业市场增长.下面是![]() 年至
年至![]() 年中国雪场滑雪人次(万人次)与同比增长率的统计图,则下面结论中不正确的是( )
年中国雪场滑雪人次(万人次)与同比增长率的统计图,则下面结论中不正确的是( )
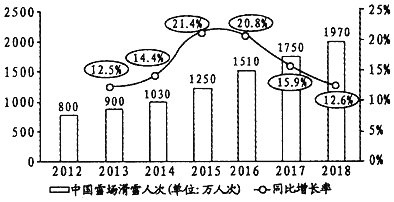
A.![]() 年至
年至![]() 年,中国雪场滑雪人次逐年增加
年,中国雪场滑雪人次逐年增加
B.![]() 年至
年至![]() 年,中国雪场滑雪人次和同比增长率均逐年增加
年,中国雪场滑雪人次和同比增长率均逐年增加
C.![]() 年与
年与![]() 年相比,中国雪场滑雪人次的同比增长率近似相等,所以同比增长人数也近似相等
年相比,中国雪场滑雪人次的同比增长率近似相等,所以同比增长人数也近似相等
D.![]() 年与
年与![]() 年相比,中国雪场滑雪人次增长率约为
年相比,中国雪场滑雪人次增长率约为![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com