【题目】设△ABC的内角A、B、C所对边的长分别为a、b、c，且有2sinBcosA=sinAcosC+cosAsinC． （Ⅰ）求角A的大小；
（Ⅱ）若b=2，c=1，D为BC的中点，求AD的长．
【答案】解：（Ⅰ）∵2sinBcosA=sinAcosC+cosAsinC ∴2sinBcosA=sin（A+C）
∵A+C=π﹣B
∴sin（A+C）=sinB＞0
∴2sinBcosA=sinB
∴cosA= 
∵A∈（0，π）
∴A= 
；
（Ⅱ）∵b=2，c=1，A=
∴a2=b2+c2﹣2bccosA=3
∴b2=a2+c2
∴B= 
∵D为BC的中点，
∴AD=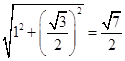 
【解析】（Ⅰ）根据2sinBcosA=sinAcosC+cosAsinC，可得2sinBcosA=sin（A+C），从而可得2sinBcosA=sinB，由此可求求角A的大小；（Ⅱ）利用b=2，c=1，A= 
，可求a的值，进而可求B= 
，利用D为BC的中点，可求AD的长．
【考点精析】本题主要考查了余弦定理的定义的相关知识点，需要掌握余弦定理:
;
;
才能正确解答此题．
科目：高中数学 来源： 题型：
【题目】设集合P={x|x2﹣x﹣6＜0}，Q={2a≤x≤a+3}．
（1）若P∪Q=P，求实数a的取值范围；
（2）若P∩Q=，求实数a的取值范围；
（3）若P∩Q={x|0≤x＜3}，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=|x+a|+|x﹣2|
（1）当a=﹣3时，求不等式f（x）≥3的解集；
（2）若f（x）≤|x﹣4|的解集包含[1，2]，求a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个多面体的直观图及三视图如图所示：（其中M，N分别是AF，BC的中点）． 
（1）求证：MN∥平面CDEF；
（2）求多面体A﹣CDEF的体积．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f (x)＝a lnx＋
＋x (a≠0)．
(1)若曲线y＝f (x)在点(1，f (1))处的切线与直线x－2y＝0垂直，求实数a的值；
(2)讨论函数f (x)的单调性．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f（x）=4cosxsin（x+
）-1．
（1）求f（x）的最小正周期和单调递减区间；
（2）将y=f（x）图象上所有的点向右平行移动个单位长度，得到y=g（x）的图象．若g（x）在（0，m）内是单调函数，求实数m的最大值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
