
����Ŀ����������й���ͳ����֮һ�����ڼ䣬�����̳�����Ʒ�Ƶ�������ս������Ȼ���죮ij�����߷��г����֣������̳���������࣬�۸�һ��������ͳ�Ʒ������õ���ij�̳���ͬ������������ۼ۸�λ��Ԫ/ǧ�ˣ���Ƶ���ֲ��������һ��ʾ��
��һ��
�۸�/��Ԫ/ǧ�ˣ� | [10��15�� | [15��20�� | [20��25�� | [25��30�� | [30��35�� |
������ | 4 | 12 | 16 | 6 | 2 |
�ڵ����У��������֣�����Ʒ�������Ϸ��滹�����˹��Σ����������������������������桢��ɳ�ȴ�ͳ�����գ��ܶ�Ʒ�ƻ��Ƴ������⡢�ɿ��������ʵ���ɫ�������ڸ��̳��ڣ����������100���˿͵���������ӿ�ζƫ�ý����˵��飬����������
������
ϲ����ͳ������ | ϲ����ɫ������ | �ܼ� | |
40������ | 30 | 15 | 45 |
40�꼰���� | 50 | 5 | 55 |
�ܼ� | 80 | 20 | 100 |
��1�����ݱ�һ���Ƹ��̳����ӵ�ƽ�����ۼۣ�ͬһ���е������ø���������е�ֵ��������
��2�����ݱ�����Ϣ�ܷ���95%�İ�����Ϊ�˿͵����ӿ�ζƫ���������йأ�
�ο���ʽ�����ݣ� ������
������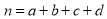 ����������
����������
P��K2��k0�� | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
 �����ҵ�����������ѧ���ӳ�����ϵ�д�
�����ҵ�����������ѧ���ӳ�����ϵ�д� ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() �İ뽹��Ϊ
�İ뽹��Ϊ![]() ��Բ
��Բ![]() ����Բ
����Բ![]() ���ҽ������������㣬ֱ��
���ҽ������������㣬ֱ��![]() ����Բ
����Բ![]() ֻ��һ��������.
ֻ��һ��������.
��1������Բ![]() �ı����̣�
�ı����̣�
��2����֪��ֱ��![]() ����Բ
����Բ![]() ����
����![]() ��������Բ
��������Բ![]() �ֱ���
�ֱ���![]() ���㣬���ʣ�
���㣬���ʣ�![]() �����Ƿ���ڶ���
�����Ƿ���ڶ���![]() ��ʹ��
��ʹ��![]() Ϊ��ֵ?�����ڣ�����ö�ֵ�͵�
Ϊ��ֵ?�����ڣ�����ö�ֵ�͵�![]() �����ꣻ�������ڣ���˵������.
�����ꣻ�������ڣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() .
.
��1����֪![]() ��
��![]() ����������
����������![]() �ļ�ֵ��
�ļ�ֵ��
��2����![]() ����
����![]() ��������㣬��a��ȡֵ��Χ.
��������㣬��a��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��������![]() ����������
����������![]() ��
��![]() ��M����n�صij���������������
��M����n�صij���������������![]() ��ΪM����.
��ΪM����.
��1�����Ȳ�����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����
����![]() �������
���ж�����![]() �Ƿ���M���У���˵�����ɣ�
�Ƿ���M���У���˵�����ɣ�
��2��������Ϊ�����ĵȱ�����![]() ��ǰ
��ǰ![]() ���Ϊ
���Ϊ![]() ����
����![]() ��֤��������
��֤��������![]() ��M���У���ָ��M��ȡֵ��Χ��
��M���У���ָ��M��ȡֵ��Χ��
��3��������![]() ��������
��������![]() �Ƿ���M���У���˵������.
�Ƿ���M���У���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ���ҽ���Ϊ
���ҽ���Ϊ![]() ����
����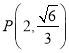 ����Բ�ϣ�
����Բ�ϣ�
��1������Բ![]() �ķ��̣�
�ķ��̣�
��2������![]() ��ֱ��
��ֱ��![]() ������Բ
������Բ![]() ��
��![]() ���㣬��
���㣬��![]() ����Բ
����Բ![]() �ϣ�����ԭ��
�ϣ�����ԭ��![]() ǡΪ
ǡΪ![]() �����ģ���ֱ��
�����ģ���ֱ��![]() �ķ��̣�
�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��{an}�ǹ��ȴ���1�ĵȱ����У�SnΪ��ǰn��ͣ�S3��7����a1+3��3a2��a3+4���ɵȲ����У�
��1��������{an}��ͨ�ʽ��
��2����bn��log2a3n+1��������{bn}��ǰn���Tn��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1����![]() ������
������![]() �ϵ����ֵ����Сֵ��
�ϵ����ֵ����Сֵ��
��2��������![]() ���Ƿ���ڵ�P��ʹ�ù���P��������ֱ��������
���Ƿ���ڵ�P��ʹ�ù���P��������ֱ��������![]() ���У������ڣ������������ȡֵ��Χ���������ڣ���˵�����ɣ�
���У������ڣ������������ȡֵ��Χ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��![]() .
.
(1)����![]() ʱ��
ʱ��![]() ȡ�ü�ֵ����
ȡ�ü�ֵ����![]() ��ֵ������
��ֵ������![]() �ĵ�������.
�ĵ�������.
(2)��![]() ����������ֵ��
����������ֵ��![]() ����
����![]() ��ȡֵ��Χ����֤����
��ȡֵ��Χ����֤����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������⣺
��������f��x�������溯������ż��������f��x����ֵ��Ϊ{0}��
��������f��x����ż��������f��|x|��=f��x����
��������f��x�����䶨�����ڲ��ǵ�����������f��x�������ڷ�������
��������f��x�����ڷ�����f��1��x������f��1��x����f��x������ȫ��ͬ����f��x����f��1��x��ͼ��Ĺ��������ֱ��y=x�ϣ�
���������������� ����д���������������ţ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com