
【题目】如图,在四校锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,边长为4的正△PAD所在平面与平面ABCD垂直,点E是AD的中点,点Q是侧棱PC的中点.

(1)求四棱锥P﹣ABCD的体积;
(2)求证:PA∥平面BDQ;
(3)在线段AB上是否存在点F,使直线PF与平面PAD所成的角为30°?若存在,求出AF的长,若不存在,请说明理由?
【答案】(1)16;(2)见解析;(3)存在,AF![]()
【解析】
(1)根据底面ABCD是菱形,且∠BAD=60°,边长为4,求面积,再由正△PAD所在平面与平面ABCD垂直,![]() ,得到
,得到![]() 平面ABCD,PE是底面上的高,然后代入体积公式求解.
平面ABCD,PE是底面上的高,然后代入体积公式求解.
(2)由O是AC中点,点Q是侧棱PC的中点,根据中位线得到OQ∥PA,再利用线面平行的判定理证明.
(3)建立空间直角坐标系,设在线段AB上存在点F,且![]() ,求得相应点的坐标,进而得到向量的坐标,再利用直线PF与平面PAD所成的角为30°,代入线面角的向量法公式求解.
,求得相应点的坐标,进而得到向量的坐标,再利用直线PF与平面PAD所成的角为30°,代入线面角的向量法公式求解.
(1)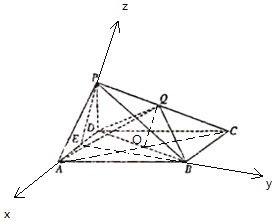
如图所示:连结PE,BE,
∵在四棱锥P﹣ABCD中,底面ABCD是菱形,∠BAD=60°,边长为4,
∴S四边形ABCD=AD×BE=4![]() 8
8![]() ,
,
又因为正△PAD所在平面与平面ABCD垂直,![]()
所以![]() 平面ABCD,
平面ABCD,
又PE![]() 2
2![]() ,
,
∴四棱锥P﹣ABCD的体积:VP﹣ABCD![]() 16.
16.
(2)证明:连结AC,BD,交于点O,连结OQ,
∵底面ABCD是菱形,∴O是AC中点,
∵点Q是侧棱PC的中点,
∴OQ∥PA,∵PA平面BDQ,OQ平面BDQ,
∴PA∥平面BDQ.
(3)以E为原点,EA为x轴,EB为y轴,EP为z轴,建立空间直角坐标系,
A(2,0,0),B(0,2![]() ,0),P(0,0,2
,0),P(0,0,2![]() ),
),
设在线段AB上存在点F,使直线PF与平面PAD所成的角为30°,
且F(a,b,c),![]() ,即(a﹣2,b,c)=(﹣2λ,2
,即(a﹣2,b,c)=(﹣2λ,2![]() ,0),λ∈[0,1],
,0),λ∈[0,1],
即a=2﹣2λ,b=2![]() λ,c=0,∴F(2﹣2λ,2
λ,c=0,∴F(2﹣2λ,2![]() ,0),
,0),
因为平面PAD的法向量![]() (0,1,0),
(0,1,0),
![]() (2﹣2
(2﹣2![]() ,﹣2
,﹣2![]() ),且直线PF与平面PAD所成的角为30°,
),且直线PF与平面PAD所成的角为30°,
∴sin30°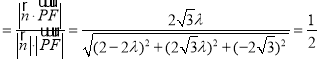 ,
,
解得![]() ,符合λ∈[0,1],
,符合λ∈[0,1],
∴AF=λAB![]() .
.
∴在线段AB上存在点F,使直线PF与平面PAD所成的角为30°,且AF![]() .
.


科目:高中数学 来源: 题型:
【题目】某小组共有![]() 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
如下表所示:
A | B | C | D | E | |
身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(Ⅰ)从该小组身高低于![]() 的同学中任选
的同学中任选![]() 人,求选到的
人,求选到的![]() 人身高都在
人身高都在![]() 以下的概率
以下的概率
(Ⅱ)从该小组同学中任选![]() 人,求选到的
人,求选到的![]() 人的身高都在
人的身高都在![]() 以上且体重指标都在
以上且体重指标都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“五一”期间,甲乙两个商场分别开展促销活动.
(Ⅰ)甲商场的规则是:凡购物满100元,可抽奖一次,从装有大小、形状相同的4个白球、4个黑球的袋中摸出4个球,中奖情况如下表:
摸出的结果 | 获得奖金(单位:元) |
4个白球或4个黑球 | 200 |
3个白球1个黑球或3个黑球1个白球 | 20 |
2个黑球2个白球 | 10 |
记![]() 为抽奖一次获得的奖金,求
为抽奖一次获得的奖金,求![]() 的分布列和期望.
的分布列和期望.
(Ⅱ)乙商场的规则是:凡购物满100元,可抽奖10次.其中,第![]() 次抽奖方法是:从编号为
次抽奖方法是:从编号为![]() 的袋中(装有大小、形状相同的
的袋中(装有大小、形状相同的![]() 个白球和
个白球和![]() 个黑球)摸出
个黑球)摸出![]() 个球,若该次摸出的
个球,若该次摸出的![]() 个球颜色都相同,则可获得奖金
个球颜色都相同,则可获得奖金![]() 元;记第
元;记第![]() 次获奖概率
次获奖概率![]() .设各次摸奖的结果互不影响,最终所获得的总奖金为10次奖金之和.
.设各次摸奖的结果互不影响,最终所获得的总奖金为10次奖金之和.
①求证:![]() ;
;
②若某顾客购买120元的商品,不考虑其它因素,从获得奖金的期望分析,他应该选择哪一家商场?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】茎叶图记录了甲,乙两组各四名同学单位时间内引体向上的次数,乙组记录中有一个数据模糊,无法确认,在图中以X表示.
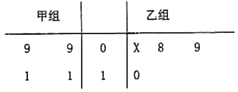
(1)如果X=8,求乙组同学单位时间内引体向上次数的平均数和方差;
(2)如果X=9,分别从甲,乙两组中随机选取一名同学,求这两名同学单位时间内引体向上次数和为19的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了普及环保知识,增强学生的环保意识,在全校组织了一次有关环保知识的竞赛.经过初赛、复赛,甲、乙两个代表队(每队3人)进入了决赛,规定每人回答一个问题,答对为本队赢得10分,答错得0分.假设甲队中每人答对的概率均为![]() ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为![]() ,
,![]() ,
,![]() ,且各人回答正确与否相互之间没有影响,用
,且各人回答正确与否相互之间没有影响,用![]() 表示乙队的总得分.
表示乙队的总得分.
(Ⅰ)求![]() 的分布列及数学期望;
的分布列及数学期望;
(Ⅱ)求甲、乙两队总得分之和等于30分且甲队获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某单位甲、乙、丙三个部门的员工人数分别为24,16,16.现采用分层抽样的方法从中抽取7人,进行睡眠时间的调查.
(I)应从甲、乙、丙三个部门的员工中分别抽取多少人?
(II)若抽出的7人中有4人睡眠不足,3人睡眠充足,现从这7人中随机抽取3人做进一步的身体检查.
(i)用X表示抽取的3人中睡眠不足的员工人数,求随机变量X的分布列与数学期望;
(ii)设A为事件“抽取的3人中,既有睡眠充足的员工,也有睡眠不足的员工”,求事件A发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】交通指数是指交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念性指数值,记交通指数为![]() ,其范围为
,其范围为![]() ,分别有五个级别:
,分别有五个级别:![]() ,畅通;
,畅通;![]() ,基本畅通;
,基本畅通;![]() ,轻度拥堵;
,轻度拥堵;![]() ,中度拥堵;
,中度拥堵;![]() ,严重拥堵.在晚高峰时段(
,严重拥堵.在晚高峰时段(![]() ),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的频率分布直方图如图所示.
),从某市交通指挥中心选取了市区20个交通路段,依据其交通指数数据绘制的频率分布直方图如图所示.

(1)求出轻度拥堵、中度拥堵、严重拥堵的路段的个数;
(2)用分层抽样的方法从轻度拥堵、中度拥堵、严重拥堵的路段中共抽取6个路段,求依次抽取的三个级别路段的个数;
(3)从(2)中抽取的6个路段中任取2个,求至少有1个路段为轻度拥堵的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com