
分析 根据两个函数的定义域相同,对应关系也相同,即可判断它们是相同函数.
解答 解:对于①,f(x)=1gx2=2lg|x|的定义域是{x|x≠0},g(x)=2lgx的定义域是{x|x>0},定义域不同,对应关系也不同,不是同一函数;
对于②,f(x)=logaax=x的定义域是R,g(x)=${a}^{lo{g}_{a}x}$=x的定义域是{x|x>0},定义域不同,不是同一函数;
对于③,f(x)=logaax=x的定义域是R,g(x)=$\root{3}{{x}^{3}}$=x的定义域是R,定义域相同,对应关系也相同,是同一函数;
对于④,f(x)=$\frac{1}{x}$的定义域是{x|x≠0},g(x)=f-1(x)=$\frac{1}{x}$的定义域是{x≠0},定义域相同,对应关系也相同,是同一函数.
综上,表示相同函数的序号是③④.
故答案为:③④.
点评 本题考查了判断两个函数是否为同一函数的应用问题,是基础题目.


科目:高中数学 来源: 题型:解答题
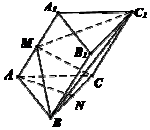 如图,在三棱锥ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,∠A1AC=60°,M,N分别是线段AA1,BC上的点,且NC=NB,AA1⊥平面BCM.
如图,在三棱锥ABC-A1B1C1中,AC=BC=AA1=2,∠ACB=90°,∠A1AC=60°,M,N分别是线段AA1,BC上的点,且NC=NB,AA1⊥平面BCM.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com