
【题目】关于函数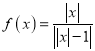 ,给出以下四个命题,其中真命题的序号是_______.
,给出以下四个命题,其中真命题的序号是_______.
①![]() 时,
时,![]() 单调递减且没有最值;
单调递减且没有最值;
②方程![]() 一定有解;
一定有解;
③如果方程![]() 有解,则解的个数一定是偶数;
有解,则解的个数一定是偶数;
④![]() 是偶函数且有最小值.
是偶函数且有最小值.
【答案】②④
【解析】
①将函数![]() 表示为分段函数,结合分式型函数的单调性进行判断;②由函数
表示为分段函数,结合分式型函数的单调性进行判断;②由函数![]() 是偶函数,在
是偶函数,在![]() 且
且![]() 时,判定函数
时,判定函数![]() 与函数
与函数![]() 在
在![]() 时有唯一交点,同理得出,当
时有唯一交点,同理得出,当![]() 且
且![]() 时,函数
时,函数![]() 与函数
与函数![]() 在
在![]() 时有交点,从而可得方程
时有交点,从而可得方程![]() 有解;③求方程
有解;③求方程![]() 的解,即可判断出命题③的正误;④利用偶函数的定义判定函数
的解,即可判断出命题③的正误;④利用偶函数的定义判定函数![]() 为偶函数,再利用绝对值的性质得出
为偶函数,再利用绝对值的性质得出![]() 且
且![]() ,即可判断出命题④的正误.
,即可判断出命题④的正误.
对于命题①,当![]() 时,
时,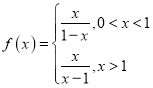 .
.
当![]() 时,
时,![]() ,则函数
,则函数![]() 在
在![]() 上单调递增,此时,
上单调递增,此时,![]() ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,则函数
,则函数![]() 在
在![]() 上单调递减,
上单调递减,
所以,当![]() 时,函数
时,函数![]() 不单调且没有最值,命题①错误;
不单调且没有最值,命题①错误;
对于命题②,当![]() 时,
时,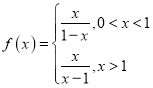 ,当
,当![]() 时,
时,![]() ,
,
当![]() 时,构造函数
时,构造函数![]() ,
,
则函数![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以,函数![]() 在
在![]() 上有且只有一个零点,
上有且只有一个零点,
即当![]() 时,方程
时,方程![]() 在
在![]() 上有解.
上有解.
函数![]() 的定义域为
的定义域为![]() ,关于原点对称,
,关于原点对称,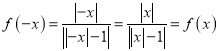 ,则函数
,则函数![]() 为偶函数,
为偶函数,
同理可知,当![]() 时,方程
时,方程![]() 在
在![]() 上有解.
上有解.
所以,命题②正确;
对于命题③,当![]() 时,令
时,令![]() ,解得
,解得![]() ,则命题③错误;
,则命题③错误;
对于命题④,由②可知,函数![]() 是偶函数,由绝对值的性质可知
是偶函数,由绝对值的性质可知![]() 且
且![]() ,则函数
,则函数![]() 为偶函数且最小值为
为偶函数且最小值为![]() ,命题④正确.
,命题④正确.
因此,正确命题的序号为②④.
故答案为:②④.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:
【题目】曲线![]() 为:到两定点
为:到两定点![]() 、
、![]() 距离乘积为常数
距离乘积为常数![]() 的动点
的动点![]() 的轨迹.以下结论正确的个数为( )
的轨迹.以下结论正确的个数为( )
(1)曲线![]() 一定经过原点;
一定经过原点;
(2)曲线![]() 关于
关于![]() 轴、
轴、![]() 轴对称;
轴对称;
(3)![]() 的面积不大于
的面积不大于![]() ;
;
(4)曲线![]() 在一个面积为
在一个面积为![]() 的矩形范围内.
的矩形范围内.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人同时参加一个外贸公司的招聘,招聘分笔试与面试两部分,先笔试后面试.甲笔试与面试通过的概率分别为0.8,0.5,乙笔试与面试通过的概率分别为0.8,0.4,且笔试通过了才能进入面试,面试通过则直接招聘录用,两人笔试与面试相互独立互不影响.
(1)求这两人至少有一人通过笔试的概率;
(2)求这两人笔试都通过却都未被录用的概率;
(3)记这两人中最终被录用的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )

A. 消耗1升汽油,乙车最多可行驶5千米
B. 以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C. 甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D. 某城市机动车最高限速80千米/小时. 相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 如图
如图![]() 的展开图如图2,其中四边形ABCD为边长等于
的展开图如图2,其中四边形ABCD为边长等于![]() 的正方形,
的正方形,![]() 和
和![]() 均为正三角形.
均为正三角形.
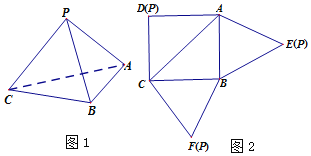
(1)证明:平面![]() 平面ABC;
平面ABC;
(2)若M是PC的中点,点N在线段PA上,且满足![]() ,求直线MN与平面PAB所成角的正弦值.
,求直线MN与平面PAB所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴.为迎接2018年“双十一”网购狂欢节,某厂家拟投入适当的广告费,对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量p万件与促销费用x万元满足![]() (其中
(其中![]() ,a为正常数).已知生产该产品还需投入成本
,a为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),每一件产品的销售价格定为
万元(不含促销费用),每一件产品的销售价格定为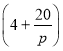 元,假定厂家的生产能力完全能满足市场的销售需求.
元,假定厂家的生产能力完全能满足市场的销售需求.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大?并求出最大利润的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() ).
).
(1)证明:当![]() 时,
时,![]() 在
在![]() 上是增函数;
上是增函数;
(2)是否存在实数![]() ,只有唯一正数
,只有唯一正数![]() ,对任意正数
,对任意正数![]() ,使不等式
,使不等式![]() 恒成立?若存在,求出这样的
恒成立?若存在,求出这样的![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于任意![]() ,若数列
,若数列![]() 满足
满足![]() ,则称这个数列为“K数列”.
,则称这个数列为“K数列”.
(1)已知数列:1,![]() ,
,![]() 是“K数列”,求实数m的取值范围;
是“K数列”,求实数m的取值范围;
(2)是否存在首项为-1的无穷等差数列![]() 为“K数列”,且其前n项和
为“K数列”,且其前n项和![]() 满足:
满足:![]() ,若存在,求出
,若存在,求出![]() 的通项公式;若不存在,请说明理由;
的通项公式;若不存在,请说明理由;
(3)已知各项均为正整数的等比数列![]() (至少有4项)为“K数列”,数列
(至少有4项)为“K数列”,数列![]() 不是“K数列”,若
不是“K数列”,若![]() ,是否存在
,是否存在![]() ,使
,使![]() 为“K数列”?若存在,请求出,
为“K数列”?若存在,请求出,![]() 若不存在,请说明理由.
若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若函数![]() 的图象经过变换
的图象经过变换![]() 后所得的图象对应的函数与
后所得的图象对应的函数与![]() 的值域相同,则称变换
的值域相同,则称变换![]() 是
是![]() 的同值变换,下面给出了四个函数与对应的变换:①
的同值变换,下面给出了四个函数与对应的变换:①![]() ,
, ![]() 将函数
将函数![]() 的图象关于直线
的图象关于直线![]() 作对称变换;②
作对称变换;②![]() ,
, ![]() 将函数
将函数![]() 的图象关于
的图象关于![]() 轴作对称变换;③
轴作对称变换;③![]() ,
, ![]() 将函数
将函数![]() 的图象关于点
的图象关于点![]() 作对称变换;④
作对称变换;④![]() ,
,![]() 将函数
将函数![]() 的图象关于点
的图象关于点![]() 作对称变换.其中
作对称变换.其中![]() 是
是![]() 的同值变换的有__________(写出所有符合题意的序号)
的同值变换的有__________(写出所有符合题意的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com