
 如图,已知三角形ABC的三边AB=4,AC=5,BC=3,椭圆M以A、B为焦点且经过点C.
如图,已知三角形ABC的三边AB=4,AC=5,BC=3,椭圆M以A、B为焦点且经过点C. 的取值范围.
的取值范围. 解:(Ⅰ)如图,以线段AB的中点为原点,以AB所在直线为x轴,建立直角坐标系,由已知设椭圆M的方程为
解:(Ⅰ)如图,以线段AB的中点为原点,以AB所在直线为x轴,建立直角坐标系,由已知设椭圆M的方程为 ,根据定义2a=AC+BC=8,2c=AB=4,b2=a2-c2,b>0
,根据定义2a=AC+BC=8,2c=AB=4,b2=a2-c2,b>0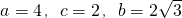
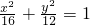 .
.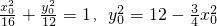

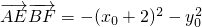 =
= =
=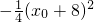
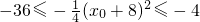
 的取值范围是[-36,-4].
的取值范围是[-36,-4].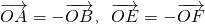
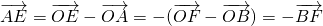
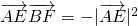 .
.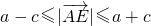 ,即
,即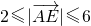 ,
,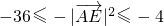
 的取值范围是[-36,-4].
的取值范围是[-36,-4]. ,由2a=AC+BC=8,2c=AB=4,能导出椭圆M的标准方程.
,由2a=AC+BC=8,2c=AB=4,能导出椭圆M的标准方程.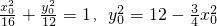 ,由A(-2,0),B(2,0),
,由A(-2,0),B(2,0), ,
,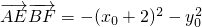 =
=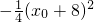 ,由此能求出
,由此能求出 的取值范围.
的取值范围.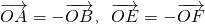 ,
,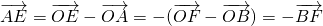 ,
,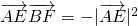 .由此能求出
.由此能求出 的取值范围.
的取值范围. 的取值范围.解题时要认真审题,注意挖掘题设中的隐含条件,注意合理地进行等价转化.
的取值范围.解题时要认真审题,注意挖掘题设中的隐含条件,注意合理地进行等价转化. 

科目:高中数学 来源: 题型:
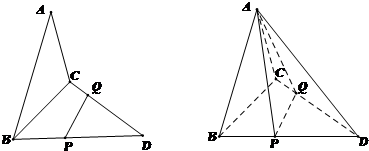 如图,已知三角形△ABC与△BCD所在平面互相垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.
如图,已知三角形△ABC与△BCD所在平面互相垂直,且∠BAC=∠BCD=90°,AB=AC,CB=CD,点P,Q分别在线段BD,CD上,沿直线PQ将△PQD向上翻折,使D与A重合.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•泉州模拟)如图,已知三角形ABC的三边AB=4,AC=5,BC=3,椭圆M以A、B为焦点且经过点C.
(2011•泉州模拟)如图,已知三角形ABC的三边AB=4,AC=5,BC=3,椭圆M以A、B为焦点且经过点C.| AE |
| BF |
查看答案和解析>>
科目:高中数学 来源: 题型:
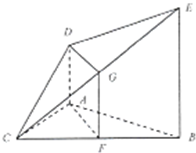 如图,已知三角形△ABC是等边三角形,AD⊥平面ABC,BE∥AD,AB=BE=2AD=2,且F、G分别是BC、CE的中点.
如图,已知三角形△ABC是等边三角形,AD⊥平面ABC,BE∥AD,AB=BE=2AD=2,且F、G分别是BC、CE的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com