
ΓΨΧβΡΩΓΩ‘ΎΡ≥¥ΈΜνΕ·÷–Θ§”–5Οϊ–“‘Υ÷°–«.’β5Οϊ–“‘Υ÷°–«Ω…ΜώΒΟ![]() ΓΔ
ΓΔ![]() ΝΫ÷÷Ϋ±ΤΖ÷–ΒΡ“Μ÷÷Θ§≤ΔΙφΕ®ΘΚΟΩΗω»ΥΆ®Ιΐ≈Ή÷ά“ΜΟΕ÷ ΒΊΨυΈΣΒΡςΜΉ”ΨωΕ®Ή‘ΦΚΉν÷’ΜώΒΟΡΡ“Μ÷÷Ϋ±ΤΖΘ®ςΜΉ”ΒΡΝυΗωΟφ…œΒΡΒψ ΐΖ÷±πΈΣ1ΒψΓΔ2ΒψΓΔ3ΒψΓΔ4ΒψΓΔ5ΒψΓΔ6ΒψΘ©Θ§≈Ή÷άΒψ ΐ–Γ”Ύ3ΒΡΜώΒΟ
ΝΫ÷÷Ϋ±ΤΖ÷–ΒΡ“Μ÷÷Θ§≤ΔΙφΕ®ΘΚΟΩΗω»ΥΆ®Ιΐ≈Ή÷ά“ΜΟΕ÷ ΒΊΨυΈΣΒΡςΜΉ”ΨωΕ®Ή‘ΦΚΉν÷’ΜώΒΟΡΡ“Μ÷÷Ϋ±ΤΖΘ®ςΜΉ”ΒΡΝυΗωΟφ…œΒΡΒψ ΐΖ÷±πΈΣ1ΒψΓΔ2ΒψΓΔ3ΒψΓΔ4ΒψΓΔ5ΒψΓΔ6ΒψΘ©Θ§≈Ή÷άΒψ ΐ–Γ”Ύ3ΒΡΜώΒΟ![]() Ϋ±ΤΖΘ§≈Ή÷άΒψ ΐ≤Μ–Γ”Ύ3ΒΡΜώΒΟ
Ϋ±ΤΖΘ§≈Ή÷άΒψ ΐ≤Μ–Γ”Ύ3ΒΡΜώΒΟ![]() Ϋ±ΤΖ.
Ϋ±ΤΖ.
Θ®1Θ©«σ’β5Οϊ–“‘Υ÷°–«÷–ΜώΒΟ![]() Ϋ±ΤΖΒΡ»Υ ΐ¥σ”ΎΜώΒΟ
Ϋ±ΤΖΒΡ»Υ ΐ¥σ”ΎΜώΒΟ![]() Ϋ±ΤΖΒΡ»Υ ΐΒΡΗ≈¬ ΘΜ
Ϋ±ΤΖΒΡ»Υ ΐΒΡΗ≈¬ ΘΜ
Θ®2Θ©…η![]() ΓΔ
ΓΔ![]() Ζ÷±πΈΣΜώΒΟ
Ζ÷±πΈΣΜώΒΟ![]() ΓΔ
ΓΔ![]() ΝΫ÷÷Ϋ±ΤΖΒΡ»Υ ΐΘ§≤ΔΦ«
ΝΫ÷÷Ϋ±ΤΖΒΡ»Υ ΐΘ§≤ΔΦ«![]() Θ§«σΥφΜζ±δΝΩ
Θ§«σΥφΜζ±δΝΩ![]() ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊ.
ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊ.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() Θ§
Θ§![]() ΒΡΖ÷≤ΦΝ–ΦϊΫβΈω.
ΒΡΖ÷≤ΦΝ–ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Ήœ»«σ≥ω5Οϊ–“‘Υ÷°–«÷–Θ§ΟΩ»ΥΜώΒΟAΫ±ΤΖΒΡΗ≈¬ ΚΆBΫ±ΤΖΒΡΗ≈¬ Θ°Θ®1Θ©ΜώΒΟAΫ±ΤΖΒΡ»Υ ΐ¥σ”ΎΜώΒΟBΫ±ΤΖΒΡ»Υ ΐΘ§ΒΟΒΫΜώΒΟAΫ±ΤΖΒΡ»Υ ΐΩ…ΡήΈΣ3Θ§4Θ§5Θ§άϊ”ΟΕάΝΔ÷ΊΗ¥ ‘―ι«σΒΟΗ≈¬ ΘΜΘ®2Θ©”…ΠΈΘΫ|X©¹Y|Θ§Ω…ΒΟΠΈΒΡΩ…Ρή»Γ÷ΒΈΣ1Θ§3Θ§5Θ§Ά§―υάϊ”ΟΕάΝΔ÷ΊΗ¥ ‘―ι«σΒΟΗ≈¬ Θ§»ΜΚσΝ–≥ωΤΒ¬ Ζ÷≤Φ±μΘ§¥ζ»κΤΎΆϊΙΪ Ϋ«σΤΎΆϊΘ°
’β5Οϊ–“‘Υ÷°–«÷–Θ§ΟΩ»ΥΜώΒΟ![]() Ϋ±ΤΖΒΡΗ≈¬ ΈΣ
Ϋ±ΤΖΒΡΗ≈¬ ΈΣ![]() Θ§
Θ§![]() Ϋ±ΤΖΒΡΗ≈¬ ΈΣ
Ϋ±ΤΖΒΡΗ≈¬ ΈΣ![]() .
.
Θ®1Θ©“ΣΜώΒΟ![]() Ϋ±ΤΖΒΡ»Υ ΐ¥σ”ΎΜώΒΟ
Ϋ±ΤΖΒΡ»Υ ΐ¥σ”ΎΜώΒΟ![]() Ϋ±ΤΖΒΡ»Υ ΐΘ§‘ρ
Ϋ±ΤΖΒΡ»Υ ΐΘ§‘ρ![]() Ϋ±ΤΖΒΡ»Υ ΐΩ…ΡήΈΣ3Θ§4Θ§5Θ§‘ρ
Ϋ±ΤΖΒΡ»Υ ΐΩ…ΡήΈΣ3Θ§4Θ§5Θ§‘ρ
Υυ«σΗ≈¬ ΈΣ![]() .
.
Θ®2Θ©![]() ΒΡΩ…Ρή»Γ÷ΒΈΣ1Θ§3Θ§5Θ§«“
ΒΡΩ…Ρή»Γ÷ΒΈΣ1Θ§3Θ§5Θ§«“![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
Υυ“‘![]() ΒΡΖ÷≤ΦΝ– «ΘΚ
ΒΡΖ÷≤ΦΝ– «ΘΚ
| 1 | 3 | 5 |
|
|
|
|
Ι ΥφΜζ±δΝΩ![]() ΒΡ ΐ―ßΤΎΆϊ
ΒΡ ΐ―ßΤΎΆϊ![]() .
.


 ΒΦ―ßΫΧ≥ΧΗΏ÷––¬ΩΈ±ξœΒΝ–¥πΑΗ
ΒΦ―ßΫΧ≥ΧΗΏ÷––¬ΩΈ±ξœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ®
Θ®![]() Θ©Θ§
Θ©Θ§![]() .
.
Θ®1Θ©»τ![]() ΒΡΆΦœσ‘Ύ
ΒΡΆΦœσ‘Ύ![]() ¥ΠΒΡ«–œΏ«ΓΚΟ“≤ «
¥ΠΒΡ«–œΏ«ΓΚΟ“≤ «![]() ΆΦœσΒΡ«–œΏ.
ΆΦœσΒΡ«–œΏ.
ΔΌ«σ Β ΐ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
ΔΎ»τΖΫ≥Χ![]() ‘Ύ«χΦδ
‘Ύ«χΦδ![]() ΡΎ”–Έ®“Μ Β ΐΫβΘ§«σ Β ΐ
ΡΎ”–Έ®“Μ Β ΐΫβΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
Θ®2Θ©Β±![]() ±Θ§«σ÷ΛΘΚΕ‘”Ύ«χΦδ
±Θ§«σ÷ΛΘΚΕ‘”Ύ«χΦδ![]() …œΒΡ»Έ“βΝΫΗω≤ΜœύΒ»ΒΡ Β ΐ
…œΒΡ»Έ“βΝΫΗω≤ΜœύΒ»ΒΡ Β ΐ![]() Θ§
Θ§ ![]() Θ§ΕΦ”–
Θ§ΕΦ”–![]() ≥…ΝΔ.
≥…ΝΔ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ(1)“―÷Σ![]() Θ§”ΟΖ÷ΈωΖ®÷ΛΟς:
Θ§”ΟΖ÷ΈωΖ®÷ΛΟς: ![]() ΘΜ
ΘΜ
(2)“―÷Σ![]() Θ§
Θ§ ![]() «“
«“![]() Θ§”ΟΖ¥÷ΛΖ®÷ΛΟς:
Θ§”ΟΖ¥÷ΛΖ®÷ΛΟς: ![]() ΕΦ¥σ”ΎΝψΘ°
ΕΦ¥σ”ΎΝψΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐfΘ®xΘ©=log4Θ®4x+1Θ©+kx”κgΘ®xΘ©=log4Θ®a2x©¹![]() aΘ©Θ§Τδ÷–fΘ®xΘ© «≈ΦΚ· ΐΘ°
aΘ©Θ§Τδ÷–fΘ®xΘ© «≈ΦΚ· ΐΘ°
Θ®1Θ©«σ Β ΐkΒΡ÷ΒΘΜ
Θ®2Θ©«σΚ· ΐgΘ®xΘ©ΒΡΕ®“ε”ρΘΜ
(3)»τΚ· ΐfΘ®xΘ©”κgΘ®xΘ©ΒΡΆΦœσ”–«“÷Μ”–“ΜΗωΙΪΙ≤ΒψΘ§«σ Β ΐaΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤![]() ΘΚ
ΘΚ![]() ΒΡΫΙΨύΈΣ8Θ§ΤδΕΧ÷αΒΡΝΫΗωΕΥΒψ”κ≥Λ÷αΒΡ“ΜΗωΕΥΒψΙΙ≥…’ΐ»ΐΫ«–ΈΓΘ
ΒΡΫΙΨύΈΣ8Θ§ΤδΕΧ÷αΒΡΝΫΗωΕΥΒψ”κ≥Λ÷αΒΡ“ΜΗωΕΥΒψΙΙ≥…’ΐ»ΐΫ«–ΈΓΘ
Θ®1Θ©«σ![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©…η![]() ΈΣ
ΈΣ![]() ΒΡΉσΫΙΒψΘ§
ΒΡΉσΫΙΒψΘ§![]() ΈΣ÷±œΏ
ΈΣ÷±œΏ![]() …œ»Έ“β“ΜΒψΘ§ΙΐΒψ
…œ»Έ“β“ΜΒψΘ§ΙΐΒψ![]() Ής
Ής![]() ΒΡ¥ΙœΏΫΜ
ΒΡ¥ΙœΏΫΜ![]() ”ΎΝΫΒψ
”ΎΝΫΒψ![]() ,
,![]() .
.
Θ®iΘ©÷ΛΟςΘΚ![]() ΤΫΖ÷œΏΕΈ
ΤΫΖ÷œΏΕΈ![]() Θ®Τδ÷–
Θ®Τδ÷–![]() ΈΣΉχ±ξ‘≠ΒψΘ©ΘΜ
ΈΣΉχ±ξ‘≠ΒψΘ©ΘΜ
Θ®iiΘ©Β±![]() »ΓΉν–Γ÷Β ±Θ§«σΒψ
»ΓΉν–Γ÷Β ±Θ§«σΒψ![]() ΒΡΉχ±ξΓΘ
ΒΡΉχ±ξΓΘ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤![]() ÷––Ρ‘Ύ‘≠ΒψΘ§ΫΙΒψ‘ΎΉχ±ξ÷α…œΘ§÷±œΏ
÷––Ρ‘Ύ‘≠ΒψΘ§ΫΙΒψ‘ΎΉχ±ξ÷α…œΘ§÷±œΏ![]() ”κΆ÷‘≤
”κΆ÷‘≤![]() ‘ΎΒΎ“ΜœσœόΡΎΒΡΫΜΒψ «
‘ΎΒΎ“ΜœσœόΡΎΒΡΫΜΒψ «![]() Θ§Βψ
Θ§Βψ![]() ‘Ύ
‘Ύ![]() ÷α…œΒΡ…δ”Α«ΓΚΟ «Ά÷‘≤
÷α…œΒΡ…δ”Α«ΓΚΟ «Ά÷‘≤![]() ΒΡ”“ΫΙΒψ
ΒΡ”“ΫΙΒψ![]() Θ§Ά÷‘≤
Θ§Ά÷‘≤![]() Νμ“ΜΗωΫΙΒψ «
Νμ“ΜΗωΫΙΒψ «![]() Θ§«“
Θ§«“![]() .
.
Θ®1Θ©«σΆ÷‘≤![]() ΒΡΖΫ≥ΧΘΜ
ΒΡΖΫ≥ΧΘΜ
Θ®2Θ©÷±œΏ![]() ΙΐΒψ
ΙΐΒψ![]() Θ§«“”κΆ÷‘≤
Θ§«“”κΆ÷‘≤![]() ΫΜ”Ύ
ΫΜ”Ύ![]() ΝΫΒψΘ§«σ
ΝΫΒψΘ§«σ![]() ΒΡΡΎ«–‘≤ΟφΜΐΒΡΉν¥σ÷Β.
ΒΡΡΎ«–‘≤ΟφΜΐΒΡΉν¥σ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() .
.
Θ®1Θ©»τ![]() «≈ΦΚ· ΐΘ§«σ
«≈ΦΚ· ΐΘ§«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©…ηΚ· ΐ![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§![]() ”–«“÷Μ”–“ΜΗω Β ΐΗυΘ§«σ
”–«“÷Μ”–“ΜΗω Β ΐΗυΘ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
Θ®3Θ©»τΙΊ”Ύ![]() ΒΡΖΫ≥Χ
ΒΡΖΫ≥Χ![]() ‘Ύ«χΦδ
‘Ύ«χΦδ![]() …œ”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυ
…œ”–ΝΫΗω≤ΜœύΒ»ΒΡ Β ΐΗυ![]() Θ§
Θ§![]() Θ§÷ΛΟςΘΚ
Θ§÷ΛΟςΘΚ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥ΜζΙΙΕ‘Ρ≥ –ΙΛ–ΫΫΉ≤ψΒΡ ’»κ«ιΩω”κ≥§«ΑœϊΖ―––ΈΣΫχ––Βς≤ιΘ§ΥφΜζ≥ι≤ιΝΥ200»ΥΘ§ΫΪΥϊΟ«ΒΡ‘¬ ’»κΘ®ΒΞΈΜΘΚΑΌ‘ΣΘ©ΤΒ ΐΖ÷≤ΦΦΑ≥§«ΑœϊΖ―ΒΡ»œΆ§»Υ ΐ’ϊάμΒΟΒΫ»γœ¬±μΗώΘΚ
‘¬ ’»κΘ®ΑΌ‘ΣΘ© |
|
|
|
|
|
|
ΤΒ ΐ | 20 | 40 | 60 | 40 | 20 | 20 |
»œΆ§≥§«ΑœϊΖ―ΒΡ»Υ ΐ | 8 | 16 | 28 | 21 | 13 | 16 |
Θ®1Θ©ΗυΨί“‘…œΆ≥ΦΤ ΐΨίΧν–¥œ¬Οφ![]() Ν–ΝΣ±μΘ§≤ΔΜΊ¥π «Ζώ”–99%ΒΡΑ―Έ’»œΈΣΒ±‘¬ ’»κ“‘8000‘ΣΈΣΖ÷ΫγΒψ ±Θ§ΗΟ –ΒΡΙΛ–ΫΫΉ≤ψΕ‘ΓΑ≥§«ΑœϊΖ―Γ±ΒΡΧ§Ε»”–≤ν“λΘΜ
Ν–ΝΣ±μΘ§≤ΔΜΊ¥π «Ζώ”–99%ΒΡΑ―Έ’»œΈΣΒ±‘¬ ’»κ“‘8000‘ΣΈΣΖ÷ΫγΒψ ±Θ§ΗΟ –ΒΡΙΛ–ΫΫΉ≤ψΕ‘ΓΑ≥§«ΑœϊΖ―Γ±ΒΡΧ§Ε»”–≤ν“λΘΜ
‘¬ ’»κ≤ΜΒΆ”Ύ8000‘Σ | ‘¬ ’»κΒΆ”Ύ8000‘Σ | ΉήΦΤ | |
»œΆ§ | |||
≤Μ»œΆ§ | |||
ΉήΦΤ |
Θ®2Θ©»τ¥”‘¬ ’»κ‘Ύ![]() ΒΡ±ΜΒς≤ιΕ‘œσ÷–ΥφΜζ―Γ»Γ2»ΥΫχ––Βς≤ιΘ§«σ÷Ν…Ό”–1Ηω»Υ≤Μ»œΆ§ΓΑ≥§«ΑœϊΖ―Γ±ΒΡΗ≈¬ .
ΒΡ±ΜΒς≤ιΕ‘œσ÷–ΥφΜζ―Γ»Γ2»ΥΫχ––Βς≤ιΘ§«σ÷Ν…Ό”–1Ηω»Υ≤Μ»œΆ§ΓΑ≥§«ΑœϊΖ―Γ±ΒΡΗ≈¬ .
≤ΈΩΦΙΪ ΫΘΚ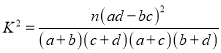 Θ®Τδ÷–
Θ®Τδ÷–![]() Θ©.
Θ©.
ΗΫ±μΘΚ
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com