
【题目】现有5名男司机,4名女司机,需选派5人运货到吴忠.
(1)如果派3名男司机、2名女司机,共有多少种不同的选派方法?
(2)至少有两名男司机,共有多少种不同的选派方法?
【答案】(1)![]() ;(2) 121.
;(2) 121.
【解析】试题分析:(1)可分步完成这件事情:第一步,选3名男司机;第二步,选2名女司机;(2)可分类完成这件事情:第一类,选2名男司机3名女司机;第二类,选3名男司机2名女司机;第三类,选4名男司机1名女司机,第四类,选25名男司机0名女司.
试题解析:(1)可分步完成这件事情:第一步,选3名男司机,有![]() 种不同的选法;第二步,选2名女司机,有
种不同的选法;第二步,选2名女司机,有![]() 种不同的选法;利用分步乘法原理,共有
种不同的选法;利用分步乘法原理,共有![]() 种不同的选法.
种不同的选法.
可分类完成这件事情:第一类,选2名男司机3名女司机,有![]() 种不同的选法;第二类,选3名男司机2名女司机,有
种不同的选法;第二类,选3名男司机2名女司机,有![]() 种不同的选法;第三类,选4名男司机1名女司机,有
种不同的选法;第三类,选4名男司机1名女司机,有![]() 种不同的选法;第四类,选5名男司机0名女司机,有
种不同的选法;第四类,选5名男司机0名女司机,有![]() 种不同的选法;
种不同的选法;
利用分类加法与分步乘法原理,共有![]() 种不同的选法..
种不同的选法..


科目:高中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x+c经过点A(0,3),B(﹣1,0),抛物线的顶点为点D,对称轴与x轴交于点E,连结BD,则抛物线表达式:BD的长为 . 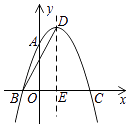
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x+2ax+b , 且f(1)= ![]() 、f(2)=
、f(2)= ![]() .
.
(1)求a、b的值;
(2)判断f(x)的奇偶性并证明;
(3)先判断并证明函数f(x)在[0,+∞)上的单调性,然后求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在矩形ABCD中, ![]() ,点
,点![]() 分别在边
分别在边![]() 上,且
上,且![]() ,
, ![]() 交
交![]() 于点
于点![]() .现将
.现将![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,得到图2.
,得到图2.
(Ⅰ)在图2中,求证: ![]() ;
;
(Ⅱ)若点![]() 是线段
是线段![]() 上的一动点,问点
上的一动点,问点![]() 在什么位置时,二面角
在什么位置时,二面角![]() 的余弦值为
的余弦值为![]() .
.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)是否存在实数![]() ,使得对任意的
,使得对任意的![]() ,都有函数
,都有函数![]() 的图象在
的图象在![]() 的图象的下方?若存在,求出最大的整数
的图象的下方?若存在,求出最大的整数![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(参考数据: ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四组函数,两个函数相同的是( )
A.f(x)= ![]() ,g(x)=x
,g(x)=x
B.f(x)=log33x , g(x)= ![]()
C.f(x)=( ![]() )2 , g(x)=|x|
)2 , g(x)=|x|
D.f(x)=x,g(x)=x0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校选择高一年级三个班进行为期二年的教学改革试验,为此需要为这三个班各购买某种设备1台.经市场调研,该种设备有甲乙两型产品,甲型价格是3000元/台,乙型价格是2000元/台,这两型产品使用寿命都至少是一年,甲型产品使用寿命低于2年的概率是![]() ,乙型产品使用寿命低于2年的概率是
,乙型产品使用寿命低于2年的概率是![]() .若某班设备在试验期内使用寿命到期,则需要再购买乙型产品更换.
.若某班设备在试验期内使用寿命到期,则需要再购买乙型产品更换.
(1)若该校购买甲型2台,乙型1台,求试验期内购买该种设备总费用恰好是10000元的概率;
(2)该校有购买该种设备的两种方案, ![]() 方案:购买甲型3台;
方案:购买甲型3台; ![]() 方案:购买甲型2台乙型1台.若根据2年试验期内购买该设备总费用的期望值决定选择哪种方案,你认为该校应该选择哪种方案?
方案:购买甲型2台乙型1台.若根据2年试验期内购买该设备总费用的期望值决定选择哪种方案,你认为该校应该选择哪种方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com