
分析 [x]表示不超过x的最大整数,分别研究等式的左边和右边,归纳出规律即可求出第n个等式的等号右边的结果.
解答 解:因为[x]表示不超过x的最大整数,
所以[$\sqrt{1}$]+[$\sqrt{2}$]+[$\sqrt{3}$]=1,[$\sqrt{4}$]+[$\sqrt{5}$]+[$\sqrt{6}$]+[$\sqrt{7}$]+[$\sqrt{8}$]=2,…,
因为等式:[$\sqrt{1}$]+[$\sqrt{2}$]+[$\sqrt{3}$]=3
[$\sqrt{4}$]+[$\sqrt{5}$]+[$\sqrt{6}$]+[$\sqrt{7}$]+[$\sqrt{8}$]=10
[$\sqrt{9}$]$+[\sqrt{10}]+[\sqrt{11}]+[\sqrt{12}]$+[$\sqrt{13}$]+[$\sqrt{14}$]+[$\sqrt{15}$]=21,
…,
所以第1个式子的左边有3项、右边1+1+1=1×3=3,
第2个式子的左边有5项、右边2+2+2+2+2=2×5=10,
第3个式子的左边有7项、右边3×7=21,
则第n个式子的左边有(2n+1)项、右边=n(2n+1)=2n2+n,即[$\sqrt{{n}^{2}}$]+[$\sqrt{{n}^{2}+1}$]+…+[$\sqrt{{n}^{2}+2n}$]=2n2+n.
故答案为:[$\sqrt{{n}^{2}}$]+[$\sqrt{{n}^{2}+1}$]+…+[$\sqrt{{n}^{2}+2n}$]=2n2+n.
点评 本题考查了归纳推理,难点在于发现其中的规律,考查观察、分析、归纳能力.


 考前必练系列答案
考前必练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
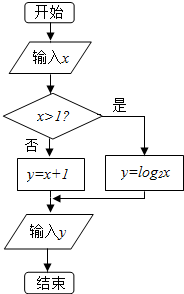
| A. | $\frac{3}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
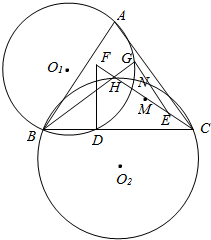 H为锐角三角形ABC的垂心,在线段CH上任取一点E,延长CH到F,使HF=CE,作FD⊥BC,EG⊥BH,其中D,G为垂足,M是线段CF的中点,O1,O2分别△ABG,△BCH的外接圆圆心,⊙O1,⊙O2的另一交点为N;证明:
H为锐角三角形ABC的垂心,在线段CH上任取一点E,延长CH到F,使HF=CE,作FD⊥BC,EG⊥BH,其中D,G为垂足,M是线段CF的中点,O1,O2分别△ABG,△BCH的外接圆圆心,⊙O1,⊙O2的另一交点为N;证明:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com