
【题目】在直角坐标系![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴,取相同长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,经过点
,经过点![]() 的动直线
的动直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,证明:
两点,证明:![]() 为定值
为定值
科目:高中数学 来源: 题型:
【题目】如图,三棱柱![]() 的底面是等边三角形,
的底面是等边三角形,![]() 在底面ABC上的射影为
在底面ABC上的射影为![]() 的重心G.
的重心G.
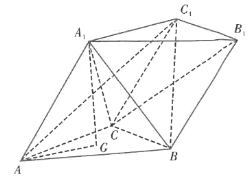
(1)已知![]() ,证明:平面
,证明:平面![]() 平面
平面![]() ;
;
(2)若三棱柱![]() 的侧棱与底面所成角的正切值为
的侧棱与底面所成角的正切值为![]() ,
,![]() ,求点
,求点![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线l的参数方程为
中,直线l的参数方程为![]() (t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]()
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)若直线l与曲线C相交于A,B两点.求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:a1=0,![]() (n∈N*),前n项和为Sn (参考数据: ln2≈0.693,ln3≈1.099),则下列选项中错误的是( )
(n∈N*),前n项和为Sn (参考数据: ln2≈0.693,ln3≈1.099),则下列选项中错误的是( )
A.![]() 是单调递增数列,
是单调递增数列,![]() 是单调递减数列B.
是单调递减数列B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正四棱锥![]() 的底面边长为
的底面边长为![]() 高为
高为![]() 其内切球与面
其内切球与面![]() 切于点
切于点![]() ,球面上与
,球面上与![]() 距离最近的点记为
距离最近的点记为![]() ,若平面
,若平面![]() 过点
过点![]() ,
,![]() 且与
且与![]() 平行,则平面
平行,则平面![]() 截该正四棱锥所得截面的面积为______.
截该正四棱锥所得截面的面积为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某病毒研究所为了更好地研究“新冠”病毒,计划改建十个实验室,每个实验室的改建费用分为装修费和设备费,每个实验室的装修费都一样,设备费从第一到第十实验室依次构成等比数列,已知第五实验室比第二实验室的改建费用高42万元,第七实验室比第四实验室的改建费用高168万元,并要求每个实验室改建费用不能超过1700万元.则该研究所改建这十个实验室投入的总费用最多需要( )
A.3233万元B.4706万元C.4709万元D.4808万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为1,线段
的棱长为1,线段![]() 上有两个动点
上有两个动点![]() ,且
,且![]() ,现有如下四个结论:
,现有如下四个结论:
![]() ;
;![]() 平面
平面![]() ;
;
![]() 三棱锥
三棱锥![]() 的体积为定值;
的体积为定值;![]() 异面直线
异面直线![]() 所成的角为定值,
所成的角为定值,
其中正确结论的序号是______.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点![]() 在椭圆
在椭圆![]() 上,过点
上,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,点
,点![]() 满足
满足![]() ,已知点
,已知点![]() 的轨迹是过点
的轨迹是过点![]() 的圆.
的圆.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(
两点(![]() ,
,![]() 在
在![]() 轴的同侧),
轴的同侧),![]() ,
,![]() 为椭圆的左、右焦点,若
为椭圆的左、右焦点,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com