
已知椭圆![]() 、抛物线
、抛物线![]() 的焦点均在
的焦点均在![]() 轴上,
轴上,![]() 的中心和
的中心和![]() 的顶点均为原点
的顶点均为原点![]() ,从每条曲线上各取两个点,将其坐标记录于下表中:
,从每条曲线上各取两个点,将其坐标记录于下表中:
|
| 3 | 2 | 4 |
|
|
|
| 0 | 4 |
|
⑴求![]() 的标准方程;
的标准方程;
⑵是否存在直线![]() 满足条件:①过
满足条件:①过![]() 的焦点
的焦点![]() ;②与
;②与![]() 交不同两点
交不同两点![]() 且满足
且满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【命题意图】本小题主要考查直线、椭圆及抛物线的标准方程,考查直线和椭圆的综合应用,考查学生的逻辑思维能力和运算求解能力.
【试题解析】解:⑴设抛物线![]() ,则有
,则有![]() ,
,
据此验证![]() 个点知(3,
个点知(3,![]() ),(4,
),(4,![]() 4)在抛物线上,易求
4)在抛物线上,易求![]() .(2分)
.(2分)
设![]() :
:![]() ,把点(
,把点(![]() 2,0),(
2,0),(![]() ,
,![]() )代入得:
)代入得:
 ,解得
,解得 .∴
.∴![]() 方程为
方程为![]() . (5分)
. (5分)
⑵容易验证直线![]() 的斜率不存在时,不满足题意. (6分)
的斜率不存在时,不满足题意. (6分)
当直线![]() 斜率存在时,假设存在直线
斜率存在时,假设存在直线![]() 过抛物线焦点
过抛物线焦点![]() ,设其方程为
,设其方程为![]() ,与
,与![]() 的交点坐标为
的交点坐标为![]() .
.
由 消去
消去![]() 并整理得
并整理得 ![]() ,
,
于是 ![]() ,
,![]() .① (8分)
.① (8分)
![]() .
.
即![]() .② (9分)
.② (9分)
由![]() ,即
,即![]() ,得
,得![]() (*).
(*).
将①、②代入(*)式,得![]() ,解得
,解得![]() ,
,
所以存在直线![]() 满足条件,且
满足条件,且![]() 的方程为:
的方程为:![]() 或
或![]() (12分)
(12分)


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:2012-2013学年湖北省八校高三第二次联考理科数学试卷(解析版) 题型:解答题
已知椭圆 ,抛物线
,抛物线 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和 的顶点均为原点
的顶点均为原点 ,每条曲线上取两个点,将其坐标记录于表中:
,每条曲线上取两个点,将其坐标记录于表中:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求 ,
, 的标准方程;
的标准方程;
(2)设斜率不为0的动直线 与
与 有且只有一个公共点
有且只有一个公共点 ,且与
,且与 的准线交于
的准线交于 ,试探究:在坐标平面内是否存在定点
,试探究:在坐标平面内是否存在定点 ,使得以
,使得以 为直径的圆恒过点
为直径的圆恒过点 ?若存在,求出
?若存在,求出 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2014届河南安阳一中高二第一次阶段测试理科数学试卷(解析版) 题型:解答题
已知椭圆 ,抛物线
,抛物线 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和 的顶点均为坐标原点
的顶点均为坐标原点 ,从每条曲线上各取两个点,将其坐标记录于表中:
,从每条曲线上各取两个点,将其坐标记录于表中:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求 的标准方程;
的标准方程;
(2)请问是否存在直线 同时满足条件:(ⅰ)过
同时满足条件:(ⅰ)过 的焦点
的焦点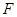 ;(ⅱ)与
;(ⅱ)与 交于不同两点
交于不同两点 、
、 ,且满足
,且满足 .若存在,求出直线
.若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省南阳市高三春期第十一次考试理科数学试卷(解析版) 题型:解答题
已知椭圆 、抛物线
、抛物线 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和 的顶点均为原点
的顶点均为原点 ,从每条曲线上取两个点,将其坐标记录于下表中:
,从每条曲线上取两个点,将其坐标记录于下表中:
|
|
3 |
|
4 |
|
|
|
|
0 |
|
|
(1)求 ,
, 的标准方程;
的标准方程;
(2)请问是否存在直线 满足条件:①过
满足条件:①过 的焦点
的焦点 ;②与
;②与 交于不同两点
交于不同两点 ,
, ,且满足
,且满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年吉林省长春市高三第一次调研测试文科数学试卷(解析版) 题型:解答题
(本小题满分12分)
已知椭圆 、抛物线
、抛物线 的焦点均在
的焦点均在 轴上,
轴上, 的中心和
的中心和 的顶点均为原点
的顶点均为原点 ,从每条曲线上各取两个点,将其坐标记录于下表中:
,从每条曲线上各取两个点,将其坐标记录于下表中:
|
|
3 |
|
4 |
|
|
|
|
0 |
|
|
⑴求 的标准方程;
的标准方程;
⑵是否存在直线 满足条件:①过
满足条件:①过 的焦点
的焦点 ;②与
;②与 交不同两点
交不同两点 且满足
且满足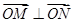 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com