(理)如果有穷数列a
1,a
2,a
3,…,a
n(n为正整数)满足条件a
1=a
n,a
2=a
n-1,…,a
n=a
1,即a
i=a
n-i+1(i=1,2,…,n),我们称其为“对称数列”.例如,由组合数组成的数列
,
,…,
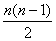
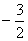
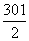
就是“对称数列”.
(1)设{bn}是项数为7的“对称数列”,其中b1,b2,b3,b4是等差数列,且b1=2,b4=11.依次写出{bn}的每一项.
(2)设{cn}是项数为2k-1(正整数k＞1)的“对称数列”,其中ck,ck+1,…,c2k-1是首项为50,公差为-4的等差数列.记{cn}各项的和为S2k-1,当k为何值时,S2k-1取得最大值?并求出S2k-1的最大值.
(3)对于确定的正整数m＞1,写出所有项数不超过2m的“对称数列”,使得1,2,22,…,2m-1依次是该数列中连续的项;当m＞1 500时,求其中一个“对称数列”前2 008项的和S2008.
(文)如果有穷数列a1,a2,a3,…,am(m为正整数)满足条件a1=am,a2=am-1,…,am=a1,即ai=am-i+1(i=1,2,…,m),我们称其为“对称数列”.例如,数列1,2,5,2,1与数列8,4,2,2,4,8都是“对称数列”.
(1)设{bn}是7项的“对称数列”,其中b1,b2,b3,b4是等差数列,且b1=2,b4=11.依次写出{bn}的每一项;
(2)设{cn}是49项的“对称数列”,其中c25,c26,…,c49是首项为1,公比为2的等比数列,求{cn}各项的和S;
(3)设{dn}是100项的“对称数列”,其中d51,d52,…,d100是首项为2,公差为3的等差数列,求{dn}前n项的和Sn(n=1,2,…,100).
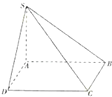（2011•许昌三模）已知四棱锥S-ABCD中，AB=BC=CD=DA=SA=2，底面ABCD是正方形，SD=SB=2
