
【题目】如图空间几何体![]() 中,
中,![]() 与
与![]() ,
,![]() 均为边长为
均为边长为![]() 的等边三角形,平面
的等边三角形,平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
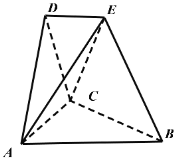
(1)试在平面![]() 内作一条直线,使得直线上任意一点
内作一条直线,使得直线上任意一点![]() 与
与![]() 的连线
的连线![]() 均与平面
均与平面![]() 平行,并给出详细证明;
平行,并给出详细证明;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯( )
A. 1盏 B. 3盏 C. 5盏 D. 9盏
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 与
与![]() 的中心在原点,焦点分别在
的中心在原点,焦点分别在![]() 轴与
轴与![]() 轴上,它们有相同的离心率
轴上,它们有相同的离心率![]() ,并且
,并且![]() 的短轴为
的短轴为![]() 的长轴,
的长轴,![]() 与
与![]() 的四个焦点构成的四边形面积是
的四个焦点构成的四边形面积是![]() .
.
(1)求椭圆![]() 与
与![]() 的方程;
的方程;
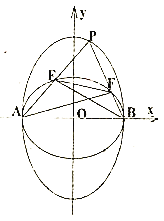
(2)设![]() 是椭圆
是椭圆![]() 上非顶点的动点,
上非顶点的动点,![]() 与椭圆
与椭圆![]() 长轴两个顶点
长轴两个顶点![]() ,
,![]() 的连线
的连线![]() ,
,![]() 分别与椭圆
分别与椭圆![]() 交于
交于![]() ,
,![]() 点.
点.
(i)求证:直线![]() ,
,![]() 斜率之积为常数;
斜率之积为常数;
(ii)直线![]() 与直线
与直线![]() 的斜率之积是否为常数?若是,求出该值;若不是,说明理由.
的斜率之积是否为常数?若是,求出该值;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解公司800名员工对公司食堂组建的需求程度,将这些员工编号为1,2,3,…,800,对这些员工使用系统抽样的方法等距抽取100人征求意见,有下述三个结论:①若25号员工被抽到,则105号员工也会被抽到;②若32号员工被抽到,则1到100号的员工中被抽取了10人;③若88号员工未被抽到,则10号员工一定未被抽到;其中正确的结论个数为( )
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com