
【题目】二项式![]() 的展开式中只有第6项的二项式系数最大,且展开式中的第3项的系数是第4项的系数的3倍,则
的展开式中只有第6项的二项式系数最大,且展开式中的第3项的系数是第4项的系数的3倍,则![]() 的值为( )
的值为( )
A. 4 B. 8 C. 12 D. 16
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某班同学利用寒假进行社会实践活动,对[25,55]岁的人群随机抽取n人进行了一次生活习惯是否符合低碳观念的调查,若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数频率分布直方图:
组数 | 分组 | 低碳族人数 | 占本组的频率 |
第一组 | [25,30) | 120 | 0.6 |
第二组 | [30,35) | 195 | p |
第三组 | [35,40) | 100 | 0.5 |
第四组 | [40,45) | a | 0.4 |
第五组 | [45,50) | 30 | 0.3 |
第六组 | [50,55) | 15 | 0.3 |

(1)补全频率分布直方图并求n、a、p的值;
(2)从年龄段在[40,50)的“低碳族”中采用分层抽样法抽取6人参加户外低碳体验活动,其中选取2人作为领队,求选取的2名领队中恰有1人年龄在[40,45)岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司今年年初用25万元引进一种新的设备,投入设备后每年收益为21万元.该公司第n年需要付出设备的维修和工人工资等费用an的信息如图. 
(1)求an;
(2)引进这种设备后,第几年后该公司开始获利;
(3)这种设备使用多少年,该公司的年平均获利最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2﹣4x﹣4y+4=0,点E(3,4).
(1)过点E的直线l与圆交与A,B两点,若AB=2 ![]() ,求直线l的方程;
,求直线l的方程;
(2)从圆C外一点P(x1 , y1)向该圆引一条切线,切点记为M,O为坐标原点,且满足PM=PO,求使得PM取得最小值时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数f(x),f′(x)是其导数,且满足f(x)+f′(x)>2,ef(1)=2e+4,则不等式exf(x)>4+2ex(其中e为自然对数的底数)的解集为( )
A.(1,+∞)
B.(﹣∞,0)∪(1,+∞)
C.(﹣∞,0)∪(0,+∞)
D.(﹣∞,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分13分)
如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(I)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(II)求证:![]() 平面
平面![]() ;
;
(II)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,有一壁画,最高点A处离地面AO=4m,最低点B处离地面BO=2m,观赏它的C点在过墙角O点与地面成30°角的射线上. 
(1)设点C到墙的距离为x,当x= ![]() m时,求tanθ的值;
m时,求tanθ的值;
(2)问C点离墙多远时,视角θ最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知一个几何体的三视图如图所示. 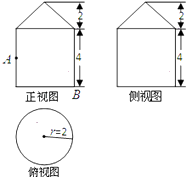
(1)求此几何体的表面积;
(2)在如图的正视图中,如果点A为所在线段中点,点B为顶点,求在几何体侧面上从点A到点B的最短路径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com