
(1)求半径为2,圆心角为![]() 的圆弧的长度.
的圆弧的长度.
(2)在半径为6的圆中,求长度为6的弦和它所对的劣弧围成的弓形面积.
(3)如图(1),在半径为10,圆心角为![]() 的扇形铁皮ADE上,截去一个半径为4的小扇形ABC,求留下部分环形的面积.
的扇形铁皮ADE上,截去一个半径为4的小扇形ABC,求留下部分环形的面积.
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:高中数学 来源:2014届四川省高二上学期期中考试数学试卷(解析版) 题型:解答题
(本题满分12分)在学校开展的综合实践活动中,某班进行了小制作评比,作品上交时间为5月1日至30日,评委会把同学们上交作品的件数按照5天一组分组统计,绘制了频率分布直方图(如图所示).已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为12,请解答下列各题.

(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件?2件作品获奖,问这两组哪一组获奖率较高?
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求半径为2,圆心角为![]() 的圆弧的长度.
的圆弧的长度.
(2)在半径为6的圆中,求长度为6的弦和它所对的劣弧围成的弓形面积.
(3)如图(1),在半径为10,圆心角为![]() 的扇形铁皮ADE上,截去一个半径为4的小扇形ABC,求留下部分环形的面积.
的扇形铁皮ADE上,截去一个半径为4的小扇形ABC,求留下部分环形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
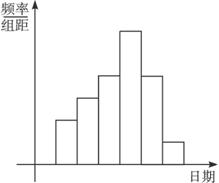
(1)本次活动共有多少件作品参加评比?
(2)哪组上交的作品数量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪一组获奖率较高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com