
分析 构造思想,sin2α=sin[(α+β)+(α-β)],cos2β=cos[(α+β)-(α-β)],利用两角和与差的公式打开计算即可求$\frac{sin2α}{cos2β}$的值.
解答 解:由tan(α+β)=2,可得$\frac{sin(α+β)}{cos(α+β)}=2$,即sin(α+β)=2cos(α+β)
tan(α-β)=3,可得$\frac{sin(α-β)}{cos(α-β)}=3$,即sin(α-β)=3cos(α-β)
sin2α=sin[(α+β)+(α-β)],cos2β=cos[(α+β)-(α-β)],
那么:$\frac{sin2α}{cos2β}$=$\frac{sin[(α+β)+(α-β)]}{cos[(α+β)-(α-β)],}$=$\frac{5}{7}$.
故答案为:$\frac{5}{7}$.
点评 本题考查两角和与差的应用,考查计算能力.


科目:高中数学 来源: 题型:解答题
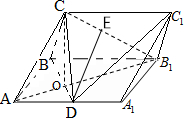 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1,E为线段B1C的中点.
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1=$\sqrt{2}$,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1,E为线段B1C的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x=0,问一开始输入的x=( )
元朝时,著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒,携着游春走,与店添一倍,逢友饮一斗,店友经三处,没了壶中酒,借问此壶中,当原多少酒?”用程序框图表达如图所示,即最终输出的x=0,问一开始输入的x=( )| A. | $\frac{3}{4}$ | B. | $\frac{7}{8}$ | C. | $\frac{15}{16}$ | D. | $\frac{31}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 商店名称 | A | B | C | D | E |
| 销售额x(千万元) | 3 | 5 | 6 | 7 | 9 |
| 利润额y(千万元) | 2 | 3 | 3 | 4 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知底面为正方形的四棱锥P-ABCD,如图(1)所示,PC⊥面ABCD,其中图(2)为该四棱锥的正(主)视图和侧(左)视图,它们是腰长为4cm的全等的等腰直角三角形.
已知底面为正方形的四棱锥P-ABCD,如图(1)所示,PC⊥面ABCD,其中图(2)为该四棱锥的正(主)视图和侧(左)视图,它们是腰长为4cm的全等的等腰直角三角形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a+b=22 | B. | a+b=21 | C. | ab=20 | D. | ab=21 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | 5 | C. | 2 | D. | 2$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com