
【题目】某种产品的广告费支出x与销售额y(单位:百万元)之间有如下的对应数据:
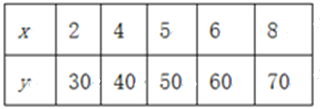
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() =
=![]() x+
x+![]() ;
;
(参考公式:用最小二乘法求线性回归方程系数公式 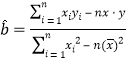 ,
,![]() .)
.)
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)根据表中所给的五组数据,得到五个点的坐标,在平面直角坐标系中画出散点图.(2 )先求出横标和纵标的平均数,得到这组数据的样本中心点,利用最小二乘法求出线性回归方程的系数,代入样本中心点求出![]() 的值,写出线性回归方程.
的值,写出线性回归方程.
试题解析:(1)散点图如下图所示:

(2)![]() ,
,![]() ,
,![]() ,
,
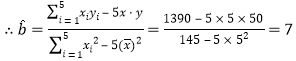 ,
,![]() ,
,
![]() 所求回归直线方程为
所求回归直线方程为![]()
【方法点晴】本题主要考查散点图的画法和线性回归方程,属于难题.求回归直线方程的步骤:①依据样本数据画出散点图,确定两个变量具有线性相关关系;②计算![]() 的值;③计算回归系数
的值;③计算回归系数![]() ;④写出回归直线方程为
;④写出回归直线方程为![]() ;(2) 回归直线过样本点中心
;(2) 回归直线过样本点中心![]() 是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.
是一条重要性质,利用线性回归方程可以估计总体,帮助我们分析两个变量的变化趋势.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ;
;
(1)若f(x)的定义域为 (-∞,+∞), 求实数a的范围;
(2)若f(x)的值域为 [0, +∞), 求实数a的范围
查看答案和解析>>
科目:高中数学 来源: 题型:
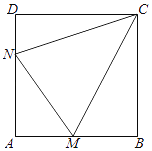
【题目】如图所示,某村积极开展“美丽乡村生态家园”建设,现拟在边长为1千米的正方形地块ABCD上划出一片三角形地块CMN建设美丽乡村生态公园,给村民休闲健身提供去处.点M,N分别在边AB,AD上. (Ⅰ)当点M,N分别是边AB,AD的中点时,求∠MCN的余弦值;
(Ⅱ)由于村建规划及保护生态环境的需要,要求△AMN的周长为2千米,请探究∠MCN是否为定值,若是,求出此定值,若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电视台举行电视奥运知识大奖赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,
初赛采用选手选一题答一题的方式进行,每位选手最多有![]() 次选题答题的机会,选手累计答对
次选题答题的机会,选手累计答对![]() 题或答错
题或答错![]() 题即终止其初赛的比赛,答对
题即终止其初赛的比赛,答对![]() 题者直接进入决赛,答错
题者直接进入决赛,答错![]() 题者则被淘汰.已知选手甲答题的正确率为
题者则被淘汰.已知选手甲答题的正确率为![]() .
.
(1) 求选手甲可进入决赛的概率;
(2) 设选手甲在初赛中答题的个数为![]() ,试写出
,试写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并与圆
外切并与圆![]() 内切,圆心
内切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求![]() 的方程;
的方程;
(2)![]() 是与圆
是与圆![]() ,圆
,圆![]() 都相切的一条直线,
都相切的一条直线,![]() 与曲线
与曲线![]() 交于
交于![]() 两点,当圆
两点,当圆![]() 的半径最长时,求
的半径最长时,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (a>0,a≠1,m≠﹣1),是定义在(﹣1,1)上的奇函数.
(a>0,a≠1,m≠﹣1),是定义在(﹣1,1)上的奇函数.
(I)求f(0)的值和实数m的值;
(II)当m=1时,判断函数f(x)在(﹣1,1)上的单调性,并给出证明;
(III)若![]() 且f(b﹣2)+f(2b﹣2)>0,求实数b的取值范围.
且f(b﹣2)+f(2b﹣2)>0,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知奇函数![]() 在区间
在区间![]() 上是增函数,且最大值为10,最小值为4,则在区间
上是增函数,且最大值为10,最小值为4,则在区间![]() 上
上![]() 的最大值、最小值分别是( )
的最大值、最小值分别是( )
A. -4,-10 B. 4,-10
C. 10,4 D. 不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com