
【题目】统计学中,经常用环比、同比来进行数据比较,环比是指本期统计数据与上期比较,如![]() 年
年![]() 月与
月与![]() 年
年![]() 月相比,同比是指本期数据与历史同时期比较,如
月相比,同比是指本期数据与历史同时期比较,如![]() 年
年![]() 月与
月与![]() 年
年![]() 月相比.
月相比.
环比增长率![]() (本期数
(本期数![]() 上期数)
上期数)![]() 上期数
上期数![]() ,
,
同比增长率![]() (本期数
(本期数![]() 同期数)
同期数)![]() 同期数
同期数![]() .
.
下表是某地区近![]() 个月来的消费者信心指数的统计数据:
个月来的消费者信心指数的统计数据:
序号 |
|
|
|
|
|
|
|
|
时间 |
|
|
|
|
|
|
|
|
消费者信心指数 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2017年
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
![]() 求该地区
求该地区![]() 年
年![]() 月消费者信心指数的同比增长率(百分比形式下保留整数);
月消费者信心指数的同比增长率(百分比形式下保留整数);
![]() 除
除![]() 年
年![]() 月以外,该地区消费者信心指数月环比增长率为负数的有几个月?
月以外,该地区消费者信心指数月环比增长率为负数的有几个月?
![]() 由以上数据可判断,序号
由以上数据可判断,序号![]() 与该地区消费者信心指数
与该地区消费者信心指数![]() 具有线性相关关系,写出
具有线性相关关系,写出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (
(![]() ,
,![]() 保留
保留![]() 位小数),并依此预测该地区
位小数),并依此预测该地区![]() 年
年![]() 月的消费者信心指数(结果保留
月的消费者信心指数(结果保留![]() 位小数,参考数据与公式:
位小数,参考数据与公式:![]() ,
,![]() ,
,![]() ,
,![]() ,
, )
)
 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】(选修4-4:坐标系与参数方程)
已知曲线C的极坐标方程是ρ=2cosθ,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线L的参数方程是 (t为参数).
(t为参数).
(1)求曲线C的直角坐标方程和直线L的普通方程;
(2)设点P(m,0),若直线L与曲线C交于A,B两点,且|PA||PB|=1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为调查某社区居民的业余生活状况,研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
休闲方式 性别 | 看电视 | 看书 | 合计 |
男 | 10 | 50 | 60 |
女 | 10 | 10 | 20 |
合计 | 20 | 60 | 80 |
(1)根据以上数据,能否有![]() 的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
的把握认为“在20:00-22:00时间段的休闲方式与性别有关系”?
(2)将此样本的频率估计为总体的概率,随机调查3名在该社区的男性,设调查的3人在这一时间段以看书为休闲方式的人数为随机变量![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式与数据![]() 对应
对应![]() ,
,![]() 对应
对应![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 。
。
Ⅰ.求函数![]() 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
Ⅱ.当![]() 时,方程
时,方程![]() 恰有两个不同的实数根,求实数
恰有两个不同的实数根,求实数![]() 的取值范围;
的取值范围;
Ⅲ.将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后所得函数
个单位后所得函数![]() 的图象关于原点中心对称,求
的图象关于原点中心对称,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
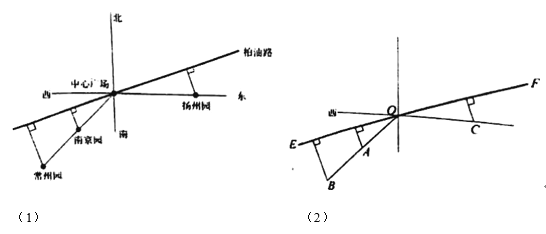
【题目】江苏省园博会有一中心广场,南京园,常州园都在中心广场的南偏西45°方向上,到中心广场的距离分别为![]() km,
km,![]() km;扬州园在中心广场的正东方向,到中心广场的距离为
km;扬州园在中心广场的正东方向,到中心广场的距离为![]() km.规划建设一条笔直的柏油路穿过中心广场,且将南京园,常州园,扬州园到柏油路的最短路径铺设成鹅卵石路(如图(1)、(2)).已知铺设每段鹅卵石路的费用(万元)与其长度的平方成正比,比例系数为2.设柏油路与正东方向的夹角,即图(2)中∠COF为
km.规划建设一条笔直的柏油路穿过中心广场,且将南京园,常州园,扬州园到柏油路的最短路径铺设成鹅卵石路(如图(1)、(2)).已知铺设每段鹅卵石路的费用(万元)与其长度的平方成正比,比例系数为2.设柏油路与正东方向的夹角,即图(2)中∠COF为![]() (
(![]() (0,
(0,![]() )),铺设三段鹅卵石路的总费用为y(万元).
)),铺设三段鹅卵石路的总费用为y(万元).
(1)求南京园到柏油路的最短距离![]() 关于
关于![]() 的表达式;
的表达式;
(2)求y的最小值及此时tan![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
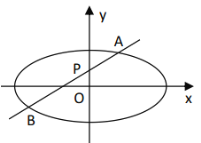
【题目】如图,椭圆![]() :
:![]() 的离心率是
的离心率是![]() ,过点
,过点![]() 的动直线
的动直线![]() 与椭圆相交于
与椭圆相交于![]() ,
,![]() 两点,当直线
两点,当直线![]() 平行
平行![]() 轴时,直线
轴时,直线![]() 被椭圆
被椭圆![]() 截得的线段长为4.
截得的线段长为4.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为坐标原点,是否存在常数
为坐标原点,是否存在常数![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com