Question

（1）设x＜y＜0，试比较（x²+y²）（x-y）与（x²-y²）•（x+y）的大小；
（2）已知a，b，c∈{正实数}，且a²+b²=c²，当n∈N，n＞2时，比较cⁿ与aⁿ+bⁿ的大小．

Answer 1

分析：（1）要求两个数的大小关系，可以对这两个数作差，通过分解因式判断差与零的关系，移项后可以得到两个式子的大小关系．
（2）本题需比较的式子是幂的形式，因此考虑用作商比较，首先作商，再用分子中的每一项除以分母，得到两个式子的和的形式，根据a²+b²=c²，两边同除以c²，根据底数的范围得到指数的大小，从而得到结果．

解答：解：（1）首先把两个要比较的式子做差，
（x²+y²）（x-y）-（x²-y²）（x+y）
=（x-y）[x²+y²-（x-y）²]
=-2xy（x-y）
∵x＜y＜0
∴xy＞0，x-y＜0，
∴-2xy（x-y）＞0
（x²+y²）（x-y）＞（x²-y²）•（x+y）
（2）∵a，b，c∈{正实数}，
∴aⁿ，bⁿ，cⁿ＞0，

an+bn

cn

= (

a

c

)n +(

b

c

)n
∵a²+b²=c²，则(

a

c

)2+(

b

c

)2=1
∴0＜

a

c

＜1，0＜

b

c

＜1
∵n∈N，n＞2，
∴(

a

c

)n＜(

a

c

)2，(

b

c

)n＜(

b

c

)2，
∴

an+bn

cn

=(

a

c

)n+(

b

c

)n＜

a2+b2

c2

=1
∴cⁿ＞aⁿ+bⁿ

点评：本题考查不等式与不等关系，考查用比较法比较两个式子的大小，若这两个式子不知符号，一般要用做差法，若是幂的形式或因式的积的形式，一般采用作商法．
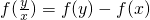