26
分析:1个平面将空间分成2部分,2个平面将空间分成4个部分,n个平面可将空间分割成
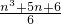
(这里不再证明),代入求解即可.
解答:首先:研究n条直线最多可将平面分割成多少个部分?(这n条直线中,任两条不平行,任三条不交于同一点),设n条直线最多可将平面分割成 b
n个部分,那么当n=1,2,3时,易知平面最多被分为2,4,7个部分.
当n=k时,设 条直线将平面分成了 b
k个部分,接着当添加上第k+1条直线时,这条直线与前 条直线相交有k个交点,这k个交点将第k条直线分割成n段,而每一段将它所在的区域一分为二,从而增加了k+1个区域,故得递推关系式b
k+1=b
k+(k+1),即b
k+1-b
k=k+1.显然当k=1时,b
1=2,当k=1,2,…(n-1)时,我们得到n-1个式子:b
2-b
1=2,b
3-b
2=3,b
4-b
3=4,…b
n-b
n-1=n
将这n-1个式子相加,得
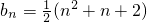
,即n条直线最多可将平面分割成
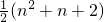
个部分.
我们来归纳一下解决这个问题的思路:从简单情形入手,确定 b
k与 b
k+1的递推关系,最后得出结论.
现在,我们回到原问题,用刚才的思路来解决空间的问题,设k个平面将空间分割成 a
k个部分,再添加上第k+1个平面,这个平面与前k个平面相交有k条交线,这k条交线,任意三条不共点,任意两条不平行,因此这第k+1个平面就被这k条直线分割成 b
k个部分.
而这 b
k个部分平面中的每一个,都把它所通过的那一部分空间分割成两个较小的空间.所以,添加上这第k+1个平面后就把原有的空间数增加了b
k 个部分.由此的递推关系式
a
k+1=a
k+b
k,即a
k+1-a
k=b
k,当k=1,2,…(n-1)时,我们得到n-1个式子:a
2-a
1=b
1,a
3-a
2=b
2,a
4-a
3=b
3,…a
n-a
n-1=b
n-1.
将这n-1个式子相加,得 a
n=a
1+(b
1+b
2+…+b
n-1),所以:
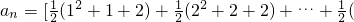
n
2+n+2)]=
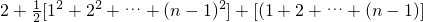
+2(n-1)}
=
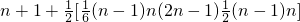
=

所以:n个平面最多可将平面分割成
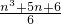
个部分.当n=5时,空间内5个平面最多可将空间分成 26个部分.
故答案为:26.
点评:本题主要考查了数字变化的一般规律问题,找出其中的内在规律,进而即可求解.

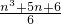 (这里不再证明),代入求解即可.
(这里不再证明),代入求解即可.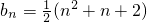 ,即n条直线最多可将平面分割成
,即n条直线最多可将平面分割成 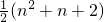 个部分.
个部分.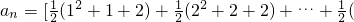 n2+n+2)]=
n2+n+2)]=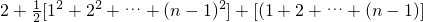 +2(n-1)}
+2(n-1)}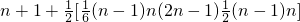 =
=
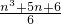 个部分.当n=5时,空间内5个平面最多可将空间分成 26个部分.
个部分.当n=5时,空间内5个平面最多可将空间分成 26个部分.
