
【题目】有一种鱼的身体吸收汞,一定量身体中汞的含量超过其体重的1.00ppm(即百万分之一)的鱼被人食用后,就会对人体产生危害.在30条鱼的样本中发现的汞含量(单位:ppm)如下:
0.07 0.24 0.95 0.98 1.02 0.98 1.37 1.40 0.39 1.02
1.44 1.58 0.54 1.08 0.61 0.72 1.20 1.14 1.62 1.68
1.85 1.20 0.81 0.82 0.84 1.29 1.26 2.10 0.91 1.31
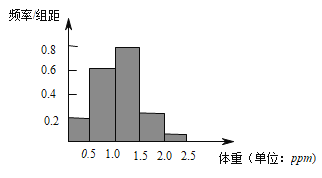
(1)请用合适的统计图描述上述数据,并分析这30条鱼的汞含量的分布特点;
(2)求出上述样本数据的平均数和标准差;
(3)从实际情况看,许多鱼的汞含量超标的原因是这些鱼在出售之前没有被检测过你认为每批这种鱼的平均承含量都比1.00ppm大吗?
(4)在上述样本中,有多少条鱼的汞含量在以平均数为中心、2倍标准差的范围内?
【答案】(1)73%在![]() 内;(2)平均数
内;(2)平均数![]() ,样本标准差
,样本标准差![]() ;(3)不一定;(4)28.
;(3)不一定;(4)28.
【解析】
(1)列出频率分布表,作出频率分布直方图;
(2)由频率分布直方图计算出样本数据的平均数和标准差的估计值;
(3)不一定能,题中数据仅仅是这一批的数据,其他批次的数据不知,这仅仅是估计值.
(4)直接确认数据在不在区间![]() 内即可.
内即可.
(1)用频率分布表如下:
分组 | 频数 | 频率 |
| 3 | 0.10 |
| 10 |
|
| 12 | 0.40 |
| 4 |
|
| 1 |
|
合计 | 30 | 1.00 |
作出统计图,这30条鱼的汞含量有约73%在![]() 内.
内.
(2)样本平均数![]() ,
,
样本方差![]()
![]()
![]() ,
,
标准差![]() ..
..
(3)不一定,因为我们不知道其他各批鱼的汞含量分布是否都和这批鱼相同,即使其他各批鱼的汞含量分布与这批鱼相同,上面的数据也只能为这个分布作出估计,不能保证每批鱼的平均汞含量都大于1.00ppm
(4)有28条鱼的汞含量在以平均数为中心、2倍标准差的范围内.


科目:高中数学 来源: 题型:
【题目】已知曲线 y = x3 + x-2 在点 P0 处的切线![]() 平行于直线
平行于直线
4x-y-1=0,且点 P0 在第三象限,
⑴求P0的坐标;
⑵若直线![]() , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,圆![]() 经过伸缩变换
经过伸缩变换![]() 后得到曲线
后得到曲线![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线
轴的正半轴为极轴,并在两种坐标系中取相同的单位长度,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程及直线
的直角坐标方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 是
是![]() 上一动点,求点
上一动点,求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M是满足下列性质的函数![]() 的全体:在定义域
的全体:在定义域![]() 内存在
内存在![]() ,使函数
,使函数![]() 成立;
成立;
(1)请给出一个![]() 的值,使函数
的值,使函数![]()
(2)函数![]() 是否是集合M中的元素?若是,请求出所有
是否是集合M中的元素?若是,请求出所有![]() 组成的集合;若不是,请说明理由;
组成的集合;若不是,请说明理由;
(3)设函数![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com