
已知函数f(x)=x2+4ax+2a+6.
(1)若函数f(x)的值域为[0,+∞),求a的值;
(2)若函数f(x)的函数值均为非负数,求g(a)=2-a|a+3|的值域.
(1) 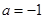 或
或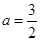 .(2)g (a)的值域为
.(2)g (a)的值域为 .
.
解析试题分析:(1)函数f(x)=x2+4ax+2a+6的值域为[0,+∞),意即这个二次函数的最小值为0,∴Δ=0,
由此便可得a的值.
(2)函数f(x)=x2+4ax+2a+6的值均为非负数,说明这个二次函数的图象的顶点在x轴上或x轴的上方,∴Δ≤0, 由此可求出a的取值范围,从而求出g(a)=2-a|a+3|的值域.
试题解析:(1)∵函数的值域为[0,+∞),
∴Δ=16a2-4(2a+6)=0, ∴2a2-a-3=0, ∴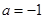 或
或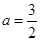 ..
..
(2)∵对一切x∈R函数值均为非负,∴Δ=8 (2a2-a -3)≤0, ∴-1≤a≤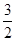 ,∴a+3>0,
,∴a+3>0,
∴g(a)=2-a|a+3|=-a2-3a+2=-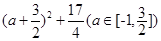 .
.
∵二次函数g (a)在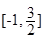 上单调递减,
上单调递减,
∴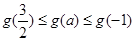 ,即-
,即-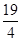 ≤g(a)≤4,∴g (a)的值域为
≤g(a)≤4,∴g (a)的值域为 .
.
考点:二次函数.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
对于函数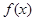 若存在
若存在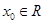 ,使得
,使得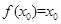 成立,则称
成立,则称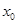 为
为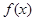 的不动点.
的不动点.
已知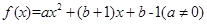
(1)当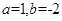 时,求函数
时,求函数 的不动点;
的不动点;
(2)若对任意实数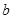 ,函数
,函数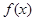 恒有两个相异的不动点,求
恒有两个相异的不动点,求 的取值范围;
的取值范围;
(3)在(2)的条件下,若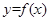 图象上
图象上 、
、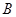 两点的横坐标是函数
两点的横坐标是函数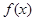 的不动点,且
的不动点,且 、
、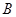 两点关于直线
两点关于直线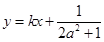 对称,求
对称,求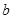 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知某公司生产品牌服装的年固定成本为10万元,每生产千件,须另投入2.7万元,设该公司年内共生产品牌服装 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为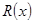 万元,且
万元,且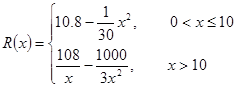 .
.
(1)写出年利润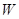 (万元)关于年产量
(万元)关于年产量 (千件)的函数解析式;
(千件)的函数解析式;
(2)当年产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
统计表明:某种型号的汽车在匀速行驶中每小时的耗油量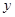 (升)关于行驶速度
(升)关于行驶速度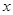 (千米/每小时)的函数解析式可以表示为
(千米/每小时)的函数解析式可以表示为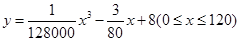 ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.
(1)当汽车以40千米/小时的速度行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大速度行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知一家公司生产某种产品的年固定成本为10万元,每生产1千件该产品需另投入2.7万元,设该公司一年内生产该产品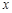 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为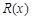 万元,且
万元,且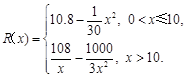
(Ⅰ)写出年利润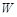 (万元)关于年产量
(万元)关于年产量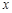 (千件)的函数解析式;
(千件)的函数解析式;
(Ⅱ)年产量为多少千件时,该公司在这一产品的产销过程中所获利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知二次函数 ,且不等式
,且不等式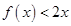 的解集为
的解集为 .
.
(1)方程 有两个相等的实根,求
有两个相等的实根,求 的解析式;
的解析式;
(2) 的最小值不大于
的最小值不大于 ,求实数
,求实数 的取值范围;
的取值范围;
(3) 如何取值时,函数
如何取值时,函数 存在零点,并求出零点.
存在零点,并求出零点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com