
2
| ||
|
| 4 |
| 9 |
| 125 |
| 729 |
| 300 |
| 729 |
| 100 |
| 243 |
| 240 |
| 729 |
| 80 |
| 243 |
| 64 |
| 729 |



 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2010年北京市丰台区高三第二次模拟考试数学(理) 题型:解答题
(13分)在某次抽奖活动中,一个口袋里装有5个白球和5个黑球,所有球除颜色外无任何不同,每次从中摸出2个球,观察颜色后放回,若为同色,则中奖。
(Ⅰ)求仅一次摸球中奖的概率;
(Ⅱ)求连续2次摸球,恰有一次不中奖的概率;
(Ⅲ)记连续3次摸球中奖的次数为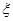 ,求
,求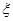 的分布列。
的分布列。
查看答案和解析>>
科目:高中数学 来源: 题型:
(13分)在某次抽奖活动中,一个口袋里装有5个白球和5个黑球,所有球除颜色外无任何不同,每次从中摸出2个球,观察颜色后放回,若为同色,则中奖。
(Ⅰ)求仅一次摸球中奖的概率;
(Ⅱ)求连续2次摸球,恰有一次不中奖的概率;
(Ⅲ)记连续3次摸球中奖的次数为![]() ,求
,求![]() 的分布列。
的分布列。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com