
【题目】已知曲线 ![]() .
.
(1)试求曲线C在点 ![]() 处的切线方程;
处的切线方程;
(2)试求与直线 ![]() 平行的曲线C的切线方程.
平行的曲线C的切线方程.
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率. 附:K2= ![]()
P(K2>k0) | 0.10 | 0.05 |
| 0.005 |
k0 | 2.706 | 3.841 |
| 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=ln(2x﹣m)的定义域为集合A,函数g(x)= ![]() ﹣
﹣ ![]() 的定义域为集合B.
的定义域为集合B.
(Ⅰ)若BA,求实数m的取值范围;
(Ⅱ)若A∩B=,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题“非空集合 ![]() 中的元素都是集合
中的元素都是集合 ![]() 中的元素”是假命题,
中的元素”是假命题,
那么下列命题中真命题的个数为( )
① ![]() 中的元素都不是
中的元素都不是 ![]() 中的元素 ②
中的元素 ② ![]() 中有不属于
中有不属于 ![]() 的元素
的元素
③ ![]() 中有属于
中有属于 ![]() 的元素 ④
的元素 ④ ![]() 中的元素不都是
中的元素不都是 ![]() 中的元素
中的元素
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=4sinωxsin(ωx+ ![]() )﹣1(ω>0),f(x)的最小正周期为π.
)﹣1(ω>0),f(x)的最小正周期为π.
(Ⅰ)当x∈[0, ![]() ]时,求f(x)的最大值;
]时,求f(x)的最大值;
(Ⅱ)请用“五点作图法”画出f(x)在[0,π]上的图象.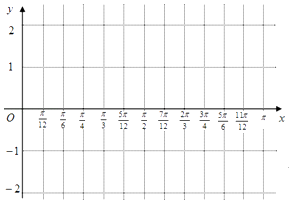
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线 ![]() 上的一点
上的一点 ![]() 的横坐标为
的横坐标为 ![]() ,焦点为
,焦点为 ![]() ,且
,且 ![]() ,直线
,直线 ![]() 与抛物线
与抛物线 ![]() 交于
交于 ![]() 两点.
两点.
(1)求抛物线 ![]() 的方程;
的方程;
(2)若 ![]() 是
是 ![]() 轴上一点,且△
轴上一点,且△ ![]() 的面积等于
的面积等于 ![]() ,求点
,求点 ![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,雾霾日趋严重,我们的工作、生活受到了严重的影响,如何改善空气质量已成为当今的热点问题.某空气净化器制造厂,决定投入生产某型号的空气净化器,根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产该型号空气净化器x(百台),其总成本为P(x)(万元),其中固定成本为12万元,并且每生产1百台的生产成本为10万元(总成本=固定成本+生产成本).销售收入Q(x)(万元)满足Q(x)= ![]() ,假定该产品产销平衡(即生产的产品都能卖掉),根据以述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据以述统计规律,请完成下列问题:
(1)求利润函数y=f(x)的解析式(利润=销售收入﹣总成本);
(2)工厂生产多少百台产品时,可使利润最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A(1,2,-1),B(2,0,2).
(1)在x轴上求一点P,使|PA|=|PB|;
(2)若xOz平面内的点M到点A的距离与到点B的距离相等,求点M的坐标满足的条件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com