
【题目】水是万物之本、生命之源,节约用水,从我做起.我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨)、一位居民的月用水量不超过
(吨)、一位居民的月用水量不超过![]() 的部分按平价收费,超出
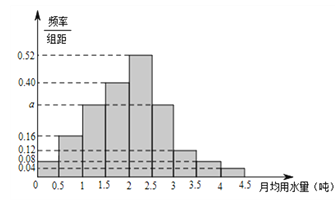
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;(3)若该市政府希望使85%的居民每月的用水量不超过标准
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5)分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;(3)若该市政府希望使85%的居民每月的用水量不超过标准![]() (吨),估计
(吨),估计![]() 的值,并说明理由.
的值,并说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 万;(3)
万;(3)![]() 吨.
吨.
【解析】试题分析:(1)根据各矩形面积和为![]() 可求得
可求得![]() 的值;(2)用水不低于
的值;(2)用水不低于![]() 吨的人分布在后三组,求出后三组的面积和即是用水不低于
吨的人分布在后三组,求出后三组的面积和即是用水不低于![]() 顿的人的概率,与总数相乘可得结果;(3)根据直方图初步判定
顿的人的概率,与总数相乘可得结果;(3)根据直方图初步判定![]() ,再利用
,再利用![]() 左边矩形面积和等于
左边矩形面积和等于![]() 可得结果.
可得结果.
试题解析:
(1)由概率统计相关知识,各组频率之和的值为1.∵频率=(频率/组距)![]() 组距
组距
∴![]() ,∴
,∴![]()
(2)由图,不低于3吨人数所占百分比为![]() ,∴全市月均用水量不低于3吨的人数为:
,∴全市月均用水量不低于3吨的人数为:![]() (万)
(万)
(3)由图可知,月均用水量小于2.5吨的居民人数所占百分比为:![]() ,即
,即![]() 的居民月均用水量小于2.5吨,同理,88%的居民月均用水量小于3吨,故
的居民月均用水量小于2.5吨,同理,88%的居民月均用水量小于3吨,故![]() ,假设月均用水量平均分布,则
,假设月均用水量平均分布,则![]() (吨).注:本次估计默认组间是平均分布,与实际可能会产生一定误差.
(吨).注:本次估计默认组间是平均分布,与实际可能会产生一定误差.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:
【题目】甲乙两人下棋比赛,规定谁比对方先多胜两局谁就获胜,比赛立即结束;若比赛进行完6局还没有分出胜负则判第一局获胜者为最终获胜且结束比赛.比赛过程中,每局比赛甲获胜的概率为![]() ,乙获胜的概率为
,乙获胜的概率为![]() ,每局比赛相互独立.求:(1)比赛两局就结束且甲获胜的概率;(2)恰好比赛四局结束的概率;(3)在整个比赛过程中,甲获胜的概率.
,每局比赛相互独立.求:(1)比赛两局就结束且甲获胜的概率;(2)恰好比赛四局结束的概率;(3)在整个比赛过程中,甲获胜的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—1:几何证明选讲
如图,已知圆![]() 是
是![]() 的外接圆,
的外接圆, ![]() ,
,![]() 是
是![]() 边上的高,
边上的高,![]() 是圆
是圆![]() 的直径,过点
的直径,过点![]() 作圆
作圆![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
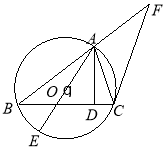
(Ⅰ)求证:![]() ;
;
(Ⅱ)若![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() (
(![]() )的右焦点为
)的右焦点为![]() ,且椭圆
,且椭圆![]() 上一点
上一点![]() 到其两焦点
到其两焦点![]() ,
,![]() 的距离之和为
的距离之和为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设直线![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() 交于不同两点
交于不同两点![]() ,
,![]() ,且
,且![]() ,若点
,若点![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com