
| 1-(x-2)2 |
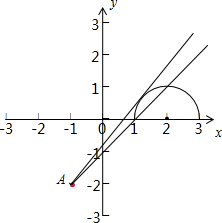 解:化简曲线y=
解:化简曲线y=| 1-(x-2)2 |
| 1-(x-2)2 |
| |3k-2| | ||
|
3+
| ||
| 4 |
3+
| ||
| 4 |
| 0+2 |
| 1+1 |
3+
| ||
| 4 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
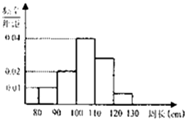 为了解一片防风林的生长情况,随机测量了其中100株树木的底部周长(单位:cm)、根据所得数据画出样品的频率分布直方图(如图),那么在这100株树木中,底部周长大于100cm的株数是
为了解一片防风林的生长情况,随机测量了其中100株树木的底部周长(单位:cm)、根据所得数据画出样品的频率分布直方图(如图),那么在这100株树木中,底部周长大于100cm的株数是查看答案和解析>>
科目:高中数学 来源: 题型:
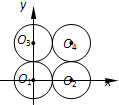 如图,有4个半径都为1的圆,其圆心分别为O1(0,0),O2(2,0),O3(0,2),O4(2,2).记集合M={⊙Oi|i=1,2,3,4}.若A,B为M的非空子集,且A中的任何一个圆与B中的任何一个圆均无公共点,则称 (A,B) 为一个“有序集合对”(当A≠B时,(A,B) 和 (B,A) 为不同的有序集合对),那么M中“有序集合对”(A,B) 的个数是( )
如图,有4个半径都为1的圆,其圆心分别为O1(0,0),O2(2,0),O3(0,2),O4(2,2).记集合M={⊙Oi|i=1,2,3,4}.若A,B为M的非空子集,且A中的任何一个圆与B中的任何一个圆均无公共点,则称 (A,B) 为一个“有序集合对”(当A≠B时,(A,B) 和 (B,A) 为不同的有序集合对),那么M中“有序集合对”(A,B) 的个数是( )| A、2 | B、4 | C、6 | D、8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 3 |
| π |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com