
【题目】已知函数f(x)的定义域是{x|x≠0},对定义域内的任意![]() ,
,![]() 都有f(
都有f(![]() ·
·![]() )=f(
)=f(![]() )+f(
)+f(![]() ),且当x>1时,f(x)>0,f(2)=1.
),且当x>1时,f(x)>0,f(2)=1.
(1)证明:![]() (x)是偶函数;
(x)是偶函数;
(2)证明:![]() (x)在(0,+∞)上是增函数;
(x)在(0,+∞)上是增函数;
(3)解不等式![]() (2
(2![]() -1)<2.
-1)<2.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)令![]() ,求得
,求得![]() ,再由
,再由![]() ,求得
,求得![]() ,进而得出
,进而得出![]() ,即可得到证明;
,即可得到证明;
(2)根据函数的单调性的定义,即可证得函数的为单调递增函数;
(3)由(1)(2)可把不等式![]() 转化为
转化为![]() ,进而得
,进而得![]() ,即可求解.
,即可求解.
(1)证明 令x1=x2=1,得f(1)=2f(1),
∴f(1)=0.令x1=x2=-1,得f(-1)=0,
∴f(-x)=f(-1·x)=f(-1)+f(x)=f(x).
∴f(x)是偶函数.
(2)证明 设x2>x1>0,
则f(x2)-f(x1)=f(x1·![]() )-f(x1)
)-f(x1)
=f(x1)+f(![]() )-f(x1)=f(
)-f(x1)=f(![]() ),
),
∵x2>x1>0,∴![]() >1.
>1.
∴f(![]() )>0,即f(x2)-f(x1)>0.
)>0,即f(x2)-f(x1)>0.
∴f(x2)>f(x1).
∴f(x)在(0,+∞)上是增函数.
(3)解 ∵f(2)=1,∴f(4)=f(2)+f(2)=2.
又∵f(x)是偶函数,
∴不等式f(2x2-1)<2可化为f(|2x2-1|)<f(4).
又∵函数f(x)在(0,+∞)上是增函数,∴|2x2-1|<4.
解得-![]() <x<
<x<![]() ,即不等式的解集为(-
,即不等式的解集为(-![]() ,
,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】为了得到函数y=sin2x的图象,只需把函数y=sin(2x﹣ ![]() )的图象( )
)的图象( )
A.向左平移 ![]() 个单位长度
个单位长度
B.向右平移 ![]() 个单位长度
个单位长度
C.向左平移 ![]() 个单位长度
个单位长度
D.向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
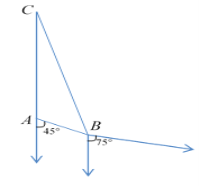
【题目】如图,在海岸A处,发现南偏东45°方向距A为(2![]() -2)海里的B处有一艘走私船,在A处正北方向,距A为
-2)海里的B处有一艘走私船,在A处正北方向,距A为![]() 海里的C处的缉私船立即奉命以10
海里的C处的缉私船立即奉命以10![]() 海里/时的速度追截走私船.
海里/时的速度追截走私船.
(1)刚发现走私船时,求两船的距离;
(2)若走私船正以10![]() 海里/时的速度从B处向南偏东75°方向逃窜,问缉私船沿什么方向能最快追上走私船?并求出所需要的时间(精确到分钟,参考数据:
海里/时的速度从B处向南偏东75°方向逃窜,问缉私船沿什么方向能最快追上走私船?并求出所需要的时间(精确到分钟,参考数据:![]() ≈1.4,
≈1.4,![]() ≈2.5).
≈2.5).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱柱![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.

(1)求四棱锥![]() 的体积;
的体积;
(2)求证: ![]() ;
;
(3)判断线段![]() 上是否存在一点
上是否存在一点![]() (与点
(与点![]() 不重合),使得
不重合),使得![]() 四点共面? (结论不要求证明)
四点共面? (结论不要求证明)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在![]() 中,角A,B,C的对边分别为a,b,c,R表示
中,角A,B,C的对边分别为a,b,c,R表示![]() 的外接圆半径.
的外接圆半径.
(Ⅰ)如图,在以O圆心、半径为2的![]() O中,BC和BA是
O中,BC和BA是![]() O的弦,其中
O的弦,其中![]() ,求弦AB的长;
,求弦AB的长;
(Ⅱ)在![]() 中,若
中,若![]() 是钝角,求证:
是钝角,求证:![]() ;
;
(Ⅲ)给定三个正实数a、b、R,其中![]() ,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的
,问:a、b、R满足怎样的关系时,以a、b为边长,R为外接圆半径的![]() 不存在、存在一个或存在两个(全等的三角形算作同一个)?在
不存在、存在一个或存在两个(全等的三角形算作同一个)?在![]() 存在的情况下,用a、b、R表示c.
存在的情况下,用a、b、R表示c.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() ,且与椭圆
,且与椭圆![]()
![]() 有相同的焦点.
有相同的焦点.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若动直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点
有且只有一个公共点![]() ,且与直线
,且与直线![]() 交于点
交于点![]() ,问:以线段
,问:以线段![]() 为直径的圆是否经过一定点
为直径的圆是否经过一定点![]() ?若存在,求出定点
?若存在,求出定点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinx,若存在x1 , x2 , …,xn满足0≤x1<x2<…<xn≤nπ,n∈N+ , 且|f(x1)﹣f(x2)|+|f(x2)﹣f(x3)|+…+|f(xm﹣1)﹣f(xm)|=12,(m≥2,m∈N+),当m取最小值时,n的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com