
(08年山东卷理)(本小题满分12分)
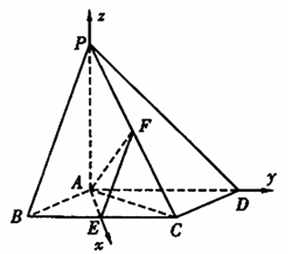
如图,已知四棱锥P-ABCD,底面ABCD为菱形,PA⊥平面ABCD,![]() ,E,F分别是BC, PC的中点.
,E,F分别是BC, PC的中点.
(Ⅰ)证明:AE⊥PD;
(Ⅱ)若H为PD上的动点,EH与平面PAD所成最大角的正切值为![]() ,求二面角E―AF―C的余弦值.
,求二面角E―AF―C的余弦值.

【解析】(Ⅰ)证明:由四边形ABCD为菱形,∠ABC=60°,可得△ABC为正三角形.
因为E为BC的中点,所以AE⊥BC.
又BC∥AD,因此AE⊥AD.
因为PA⊥平面ABCD,AE![]() 平面ABCD,所以PA⊥AE.
平面ABCD,所以PA⊥AE.
而PA![]() 平面PAD,AD
平面PAD,AD![]() 平面PAD 且PA∩AD=A,
平面PAD 且PA∩AD=A,
所以AE⊥平面PAD,又PD![]() 平面PAD.
平面PAD.
所以 AE⊥PD.

(Ⅱ)解:设AB=2,H为PD上任意一点,连接AH,EH.
由(Ⅰ)知AE⊥平面PAD,
则∠EHA为EH与平面PAD所成的角.
在Rt△EAH中,AE=![]() ,
,
所以 当AH最短时,∠EHA最大,
即 当AH⊥PD时,∠EHA最大.
此时tan∠EHA=![]()
因此AH=![]() .又AD=2,所以∠ADH=45°,
.又AD=2,所以∠ADH=45°,
所以 PA=2.
解法一:因为PA⊥平面ABCD,PA![]() 平面PAC,
平面PAC,
所以平面PAC⊥平面ABCD.
过E作EO⊥AC于O,则EO⊥平面PAC,
过O作OS⊥AF于S,连接ES,则∠ESO为二面角E-AF-C的平面角,
在Rt△AOE中,EO=AE?sin30°=![]() ,AO=AE?cos30°=
,AO=AE?cos30°=![]() ,
,
又F是PC的中点,在Rt△ASO中,SO=AO?sin45°=![]() ,
,
又 ![]()
在Rt△ESO中,cos∠ESO=
即所求二面角的余弦值为![]()
解法二:由(Ⅰ)知AE,AD,AP两两垂直,以A为坐标原点,建立如图所示的空间直角坐标系,又E、F分别为BC、PC的中点,所以
E、F分别为BC、PC的中点,所以
A(0,0,0),B(![]() ,-1,0),C(C,1,0),
,-1,0),C(C,1,0),
D(0,2,0),P(0,0,2),E(![]() ,0,0),F(
,0,0),F(![]() ),
),
所以 ![]()
设平面AEF的一法向量为![]()
则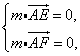
因此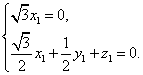
取![]()
![]()
因为 BD⊥AC,BD⊥PA,PA∩AC=A,
所以 BD⊥平面AFC,
故 ![]() 为平面AFC的一法向量.
为平面AFC的一法向量.
又 ![]() =(-
=(-![]() ),
),
所以 cos<m, ![]()
![]()
因为二面角E-AF-C为锐角,
所以所求二面角的余弦值为![]()
![]()


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
(7)(08年山东卷理)在某地的奥运火炬传递活动中,有编号为1,2,3,…,18的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成3为公差的等差数列的概率为
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(7)(08年山东卷理)在某地的奥运火炬传递活动中,有编号为1,2,3,…,18的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成3为公差的等差数列的概率为
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年山东卷理)右图是根据《山东统计年整2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字,从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为
(A)304.6 (B)303.6 (C)302.6 (D)301.6

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com