
【题目】如图所示,MCN是某海湾旅游区的一角,为营造更加优美的旅游环境,旅游区管委会决定建立面积为4 ![]() 平方千米的三角形主题游戏乐园ABC,并在区域CDE建立水上餐厅.已知∠ACB=120°,∠DCE=30°.
平方千米的三角形主题游戏乐园ABC,并在区域CDE建立水上餐厅.已知∠ACB=120°,∠DCE=30°.
(1)设AC=x,AB=y,用x表示y,并求y的最小值;
(2)设∠ACD=θ(θ为锐角),当AB最小时,用θ表示区域CDE的面积S,并求S的最小值.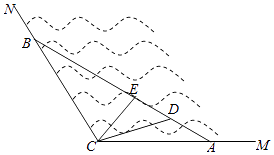
【答案】
(1)解:∵AC=x,AB=y,∠ACB=120°,
S△ABC= ![]() ACBCsin120°=
ACBCsin120°= ![]() =4
=4 ![]() ,
,
∴BC= ![]() .
.
△ABC中,利用余弦定理可得AB2=AC2+BC2﹣2ACBCcos120°,
即y2=x2+ ![]() +16≥2
+16≥2 ![]() +16=48,
+16=48,
∴y≥4 ![]() ,当且仅当x2=16,即x=4时,取等号,
,当且仅当x2=16,即x=4时,取等号,
故当x=4时,y取得最小值为4 ![]() .
.
(2)解:设∠ACD=θ(θ为锐角),
当AB最小时,x=AC=4=BC,AB=4 ![]() ,∠CAB=∠CBA=30°,
,∠CAB=∠CBA=30°,
△ACD中,由正弦定理可得 ![]() =
= ![]() ,
,
∴CD= ![]() =
= ![]() =
= ![]() ,
,
△ACE中,由正弦定理可得CE= ![]() =
= ![]() =
= ![]() ,
,
根据区域CDE的面积S= ![]() CDCEsin30°=
CDCEsin30°= ![]() =
= ![]() ,
,
故当2θ= ![]() ,即θ=
,即θ= ![]() 时,区域CDE的面积S取得最小值为
时,区域CDE的面积S取得最小值为 ![]() =8﹣4
=8﹣4 ![]() .
.
【解析】1、根据题意可设AC=x,AB=y利用余弦定理求得BC的值即得y的函数解析式再利用基本不等式求得y的最小值。
2、由题意可知在△ACD中根据正弦定理求得CD的值在△ACE中再根据正弦定理求得CE的值。根据区域CDE的面积S=![]() ,利用正弦函数的值域求得区域CDE的面积最小值。
,利用正弦函数的值域求得区域CDE的面积最小值。


科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB、PB的中点 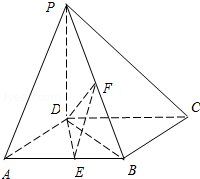
(1)求证:EF⊥CD;
(2)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论;
(3)求DB与平面DEF所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设x,y满足约束条件 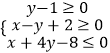 ,且目标函数z=ax+y仅在点(4,1)处取得最大值,则原点O到直线ax﹣y+17=0的距离d的取值范围是( )
,且目标函数z=ax+y仅在点(4,1)处取得最大值,则原点O到直线ax﹣y+17=0的距离d的取值范围是( )
A.(4 ![]() ,17]
,17]
B.(0,4 ![]() )
)
C.( ![]() ,17]
,17]
D.(0, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个命题:
①对立事件一定是互斥事件;
②函数y=x+ ![]() 的最小值为2;
的最小值为2;
③八位二进制数能表示的最大十进制数为256;
④在△ABC中,若a=80,b=150,A=30°,则该三角形有两解.
其中正确命题的个数为( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某赛季甲、乙两位运动员每场比赛得分的茎叶图如图所示:
(1)从甲、乙两人的这5次成绩中各随机抽取一个,求甲的成绩比乙的成绩高的概率;
(2)试用统计学中的平均数、方差知识对甲、乙两位运动员的测试成绩进行分析.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}的前n项和记为Sn , a1=t,an+1=2Sn+1(n∈N*).
(1)当t为何值时,数列{an}为等比数列?
(2)在(1)的条件下,若等差数列{bn}的前n项和Tn有最大值,且T3=15,又a1+b1 , a2+b2 , a3+b3成等比数列,求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于数列{an},定义Hn= ![]() 为{an}的“优值”,现在已知某数列{an}的“优值”Hn=2n+1 , 记数列{an﹣kn}的前n项和为Sn , 若Sn≤S5对任意的n(n∈N*)恒成立,则实数k的取值范围为 .
为{an}的“优值”,现在已知某数列{an}的“优值”Hn=2n+1 , 记数列{an﹣kn}的前n项和为Sn , 若Sn≤S5对任意的n(n∈N*)恒成立,则实数k的取值范围为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD的平行四边形,∠ADC=60°, ![]() ,PA⊥面ABCD,E为PD的中点.
,PA⊥面ABCD,E为PD的中点.
(Ⅰ)求证:AB⊥PC
(Ⅱ)若PA=AB= ![]() ,求三棱锥P﹣AEC的体积.
,求三棱锥P﹣AEC的体积.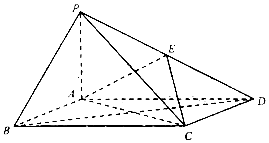
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y= ![]() sin2x+cos2x的图象,只需将函数y=2sin2x的图象( )
sin2x+cos2x的图象,只需将函数y=2sin2x的图象( )
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com