
【题目】已知抛物线![]() 的焦点为
的焦点为![]() , 直线
, 直线![]() 过点
过点![]() .
.
(Ⅰ)若点![]() 到直线
到直线![]() 的距离为
的距离为![]() , 求直线
, 求直线![]() 的斜率;
的斜率;
(Ⅱ)设![]() 为抛物线上两点, 且
为抛物线上两点, 且![]() 不与
不与![]() 轴垂直, 若线段
轴垂直, 若线段![]() 的垂直平分线恰过点
的垂直平分线恰过点![]() , 求证: 线段
, 求证: 线段![]() 中点的横坐标为定值.
中点的横坐标为定值.
【答案】(Ⅰ) ![]() (Ⅱ)详见解析
(Ⅱ)详见解析
【解析】
试题分析:(Ⅰ)设直线l的方程为y=k(x-4),由已知,抛物线C的焦点坐标为(1,0),因为点F到直线l的距离为![]() ,所以
,所以![]() ,由此能求出直线l的斜率;(Ⅱ)设线段AB中点的坐标为N
,由此能求出直线l的斜率;(Ⅱ)设线段AB中点的坐标为N![]() ,A
,A![]() ,B
,B![]() ,因为AB不垂直于x轴,所以直线MN的斜率为
,因为AB不垂直于x轴,所以直线MN的斜率为![]() ,直线AB的斜率为
,直线AB的斜率为![]() ,直线AB的方程为
,直线AB的方程为![]() ,由此能够证明线段AB中点的横坐标为定值
,由此能够证明线段AB中点的横坐标为定值
试题解析:(Ⅰ)由已知,x=4不合题意.设直线l的方程为y=k(x-4),
由已知,抛物线C的焦点坐标为(1,0),
因为点F到直线l的距离为![]() ,
,
所以![]() ,
,
解得![]() ,所以直线l的斜率为
,所以直线l的斜率为![]() .
.
(Ⅱ) 设线段![]() 中点的坐标为
中点的坐标为![]() ,
, ![]() ,
,
因为![]() 不垂直于
不垂直于![]() 轴,
轴,
则直线![]() 的斜率为
的斜率为![]() , 直线
, 直线![]() 的斜率为
的斜率为![]() ,
,
直线![]() 的方程为
的方程为![]() ,
,
联立方程
消去![]() 得
得![]() ,
,
所以![]() ,
,
因为![]() 为
为![]() 中点, 所以
中点, 所以![]() , 即
, 即![]() ,
,
所以![]() .即线段
.即线段![]() 中点的横坐标为定值
中点的横坐标为定值![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() ,直线
,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,
两点, ![]() 的周长为16,
的周长为16, ![]() 的周长为12.
的周长为12.
(1)求椭圆![]() 的标准方程与离心率;
的标准方程与离心率;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 是线段
是线段![]() 的中点,求直线
的中点,求直线![]() 的一般方程.
的一般方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的前n项和为Sn,且满足Sn=2n+1+2p(n∈N*).
(1)求p的值及数列{an}的通项公式;
(2)若数列{bn}满足![]() =(3+p)anbn,求数列{bn}的前n项和Tn.
=(3+p)anbn,求数列{bn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,f(x)=2sin(x-A)cosx+sin(B+C)(x∈R),函数f(x)的图象关于点![]() 对称.
对称.
(1)当![]() 时,求f(x)的值域;
时,求f(x)的值域;
(2)若a=7且![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人为研究中学生的性别与每周课外阅读量这两个变量的关系,随机抽查了100名中学生,得到频率分布直方图(如图所示),其中样本数据的分组区间为:[0,2],(2,4],(4,6],(6,8],(8,10],(10,12].

(Ⅰ)假设同一组中的每个数据可用该组区间的中点值代替,试估计样本中的100名学生周课外阅读时间的平均数.
(Ⅱ)在样本数据中,有20位女生的每周课外阅读时间超过4小时,15位男生的每周课外阅读时间没有超过4小时.请画出每周课外阅读时间与性别列联表,并判断能否在犯错误的概率不超过0.05的前提下认为“该校学生的每周课外阅读时间与性别有关”.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
附: 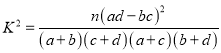
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2016·无锡模拟)已知函数f(x)满足![]() ,当x∈[0,1]时,f(x)=x.若g(x)=f(x)-mx-2m在区间(-1,1]上有两个零点,则实数m的取值范围是________________.
,当x∈[0,1]时,f(x)=x.若g(x)=f(x)-mx-2m在区间(-1,1]上有两个零点,则实数m的取值范围是________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2018·日照一模)如图所示,ABCD-A1B1C1D1是长方体,O是B1D1的中点,直线A1C交平面AB1D1于点M,给出下列结论:

①A、M、O三点共线;②A、M、O、A1不共面;③A、M、C、O共面;④B、B1、O、M共面.
其中正确结论的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正项等差数列{an}满足a1=4,且a2,a4+2,2a7-8成等比数列,{an}的前n项和为Sn.
(1)求数列{an}的通项公式;
(2)令![]() ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com