
【题目】某市为了制定合理的节电方案,供电局对居民用电进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:度),将数据按照![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.
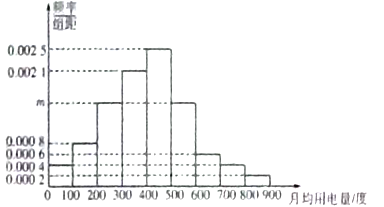
(Ⅰ)求直方图中![]() 的值并估计居民月均用电量的中位数;
的值并估计居民月均用电量的中位数;
(Ⅱ)现从第8组和第9组的居民中任选取2户居民进行访问,则两组中各有一户被选中的概率.
【答案】(Ⅰ)![]() .中位数为408度.(Ⅱ)
.中位数为408度.(Ⅱ) ![]() .
.
【解析】试题分析:(1)根据频率分布直方图,求解![]() 的值,即可求得前4组的频率之和,从而估计出居民的月均用电量的中位数;
的值,即可求得前4组的频率之和,从而估计出居民的月均用电量的中位数;
(2)计算出第8和第9组的户数,分别设为![]() 和
和![]() ,从而得到选出2户的基本事件的个数,进而得到两组中各有一户被选中的基本事件个数,利用古典概型的概率计算公式,即可求解概率。
,从而得到选出2户的基本事件的个数,进而得到两组中各有一户被选中的基本事件个数,利用古典概型的概率计算公式,即可求解概率。
试题解析:
解:(Ⅰ) ![]() ,
,
∴![]() .
.
设中位数是![]() 度,前5组的频率之和为
度,前5组的频率之和为![]() ,
,
而前4组的频率之和为![]() ,
,
所以![]() ,
, ![]() ,
,
故![]() ,即居民月均用电量的中位数为408度.
,即居民月均用电量的中位数为408度.
(Ⅱ)第8组的户数为![]() ,分别设为
,分别设为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,第9组的户数为
,第9组的户数为![]() ,分别设为
,分别设为![]() ,
, ![]() ,则从中任选出2户的基本事件为
,则从中任选出2户的基本事件为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共15种.
共15种.
其中两组中各有一户被选中的基本事件为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共8种.
共8种.
所以第8,9组各有一户被选中的概率![]() .
.


科目:高中数学 来源: 题型:
【题目】某商品的进价为每件![]() 元,售价为每件
元,售价为每件![]() 元,每个月可卖出
元,每个月可卖出![]() 件;如果每件商品在该售价的基础上每上涨
件;如果每件商品在该售价的基础上每上涨![]() 元,则每个月少卖
元,则每个月少卖![]() 件(每件售价不能高于
件(每件售价不能高于![]() 元).设每件商品的售价上涨
元).设每件商品的售价上涨![]() 元(
元(![]() 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数的函数关系式并直接写出自变量
的函数的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作抛物线
作抛物线![]() 的两条切线, 切点分别为
的两条切线, 切点分别为![]() ,
, ![]() .
.
(1) 证明: ![]() 为定值;
为定值;
(2) 记△![]() 的外接圆的圆心为点
的外接圆的圆心为点![]() , 点
, 点![]() 是抛物线
是抛物线![]() 的焦点, 对任意实数
的焦点, 对任意实数![]() , 试判断以
, 试判断以![]() 为直径的圆是否恒过点
为直径的圆是否恒过点![]() ? 并说明理由.
? 并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一种新型的洗衣液,去污速度特别快.已知每投放k(1≤k≤4,且k∈R)个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度y(克/升)随着时间x(分钟)变化的函数关系式近似为y=k·f(x),其中f(x)=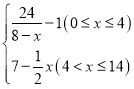 若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
(1)若只投放一次k个单位的洗衣液,两分钟时水中洗衣液的浓度为3(克/升),求k的值;
(2)若只投放一次4个单位的洗衣液,则有效去污时间可达几分钟?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2sin(x-![]() )-
)-![]() ,现将f(x)的图象向左平移
,现将f(x)的图象向左平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度,得到函数g(x)的图象.
个单位长度,得到函数g(x)的图象.
(1)求f(![]() )+g(
)+g(![]() )的值;
)的值;
(2)若a,b,c分别是△ABC三个内角A,B,C的对边,a+c=4,且当x=B时,g(x)取得最大值,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
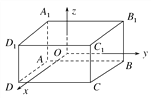
【题目】如图,已知长方体ABCD-A1B1C1D1的对称中心在坐标原点,交于同一顶点的三个面分别平行于三个坐标平面,顶点A(-2,-3,-1),求其他七个顶点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知直线方程为(2+m)x+(1-2m)y+4-3m=0,求证:不论m为何实数,此直线必过定点;
(2)过这定点引一直线,使它夹在两坐标轴间的线段被这点平分,求这条直线的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com