
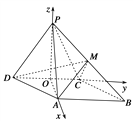
【题目】如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ADC=60°,侧面PDC是正三角形,平面PDC⊥平面ABCD,CD=2,M为PB的中点.

(1)求证:PA⊥平面CDM.
(2)求二面角D-MC-B的余弦值.
【答案】(1) 见解析;(2)-![]() .
.
【解析】试题分析:
(1)取DC中点O,连接PO,根据题意可证得OA,OC,OP两两垂直,建立空间直角坐标系,运用坐标法可证得![]() ,从而PA⊥DM,PA⊥DC,根据线面垂直的判定定理可得结论.(2)结合(1)可求得平面BMC的一个法向量
,从而PA⊥DM,PA⊥DC,根据线面垂直的判定定理可得结论.(2)结合(1)可求得平面BMC的一个法向量![]() ,又平面CDM的法向量为
,又平面CDM的法向量为![]() ,求出两向量夹角的余弦值,结合图形可得二面角的余弦值.
,求出两向量夹角的余弦值,结合图形可得二面角的余弦值.
试题解析:
(1)取DC中点O,连接PO.
∵侧面PDC是正三角形,
∴PO⊥DC,
又平面PDC⊥平面ABCD,平面PDC∩平面ABCD=DC,
∴PO⊥底面ABCD.
又底面ABCD为菱形,且∠ADC=60°,DC=2,
∴DO=1,OA⊥DC.
以O为原点,分别以OA,OC,OP所在直线为x轴,y轴,z轴,建立如图所示的空间直角坐标系O-xyz.

则![]() ,
,  ,
,
∴ ,
,
∴![]() ,
,
∴PA⊥DM,PA⊥DC,
又DM∩DC=D,
∴PA⊥平面CDM.
(2)由(1)得 ,
,
设平面BMC的一个法向量![]() ,
,
由 ,得
,得 ,
,
令z=1,得![]() .
.
由(1)知平面CDM的法向量为![]() ,
,
∴ ,
,
由图形知二面角D-MC-B是钝角,
所以二面角D-MC-B的余弦值为![]() .
.


 培优口算题卡系列答案
培优口算题卡系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以
),以![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设![]() ,直线
,直线![]() 交曲线
交曲线![]() 于
于![]() 两点,
两点,![]() 是直线
是直线![]() 上的点,且
上的点,且![]() ,当
,当![]() 最大时,求点
最大时,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}的各项均为正数,且a1+2a2=5,4a=a2a6.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足b1=2,且bn+1=bn+an,求数列{bn}的通项公式;
(3)设![]() ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,面CDEF为正方形,面ABCD为等腰梯形,AB∥CD,AC=![]() ,AB=2BC=2,AC⊥FB.
,AB=2BC=2,AC⊥FB.

(1)求证:AC⊥平面FBC;
(2)求四面体FBCD的体积;
(3)线段AC上是否存在点M,使得EA∥平面FDM?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2-2ax+5.
(1)若f(x)的定义域和值域均是[1,a],求实数a的值;
(2)若a≤1,求函数y=|f(x)|在[0,1]上的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,AB∥CD ,且∠BAP=∠CDP =90°.

(1).证明:平面PAB⊥平面PAD;
(2).若PA=PD=AB=DC, ∠APD =90°,且四棱锥PABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“剑桥学派”创始人之一数学家哈代说过:“数学家的造型,同画家和诗人一样,也应当是美丽的”;古希腊数学家毕达哥拉斯创造的“黄金分割”给我们的生活处处带来美;我国古代数学家赵爽创造了优美“弦图”.“弦图”是由四个全等的直角三角形与一个小正方形拼成的一个大正方形,如果小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为![]() ,则
,则![]() 等于( )
等于( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以平面直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程是
的参数方程是![]() ,(
,(![]() 为参数).
为参数).
(1)求直线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com