
【题目】若函数f(x)=x2﹣ ![]() 在其定义域内的一个子区间(k﹣1,k+1)内不是单调函数,则实数k的取值范围( )
在其定义域内的一个子区间(k﹣1,k+1)内不是单调函数,则实数k的取值范围( )
A.[1,+∞)
B.[1, ![]() )
)
C.[1,+2)
D.![]()
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() +
+ ![]() =1(a>b>0)右顶点与右焦点的距离为
=1(a>b>0)右顶点与右焦点的距离为 ![]() ﹣1,短轴长为2
﹣1,短轴长为2 ![]() . (Ⅰ)求椭圆的方程;
. (Ⅰ)求椭圆的方程;
(Ⅱ)过左焦点F的直线与椭圆分别交于A、B两点,若三角形OAB的面积为 ![]() ,求直线AB的方程.
,求直线AB的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() 、
、 ![]() 为平面向量,若存在不全为零的实数λ,μ使得λ
为平面向量,若存在不全为零的实数λ,μ使得λ ![]() +μ
+μ ![]() =0,则称
=0,则称 ![]() 、
、 ![]() 线性相关,下面的命题中,
线性相关,下面的命题中, ![]() 、
、 ![]() 、
、 ![]() 均为已知平面M上的向量. ①若
均为已知平面M上的向量. ①若 ![]() =2
=2 ![]() ,则
,则 ![]() 、
、 ![]() 线性相关;
线性相关;
②若 ![]() 、
、 ![]() 为非零向量,且
为非零向量,且 ![]() ⊥
⊥ ![]() ,则
,则 ![]() 、
、 ![]() 线性相关;
线性相关;
③若 ![]() 、
、 ![]() 线性相关,
线性相关, ![]() 、
、 ![]() 线性相关,则
线性相关,则 ![]() 、
、 ![]() 线性相关;
线性相关;
④向量 ![]() 、
、 ![]() 线性相关的充要条件是
线性相关的充要条件是 ![]() 、
、 ![]() 共线.
共线.
上述命题中正确的是(写出所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五面体ABCDEF中,FA⊥平面ABCD,AD∥BC∥FE,AB⊥AD,M为EC的中点,AF=AB=BC=FE= ![]() AD.
AD. 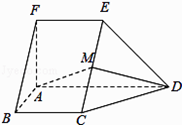
(1)求异面直线BF与DE所成的角的大小;
(2)证明平面AMD⊥平面CDE;
(3)求锐二面角A﹣CD﹣E的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间四边形ABCD中,E,F,G分别是AB,BC,CD的中点, 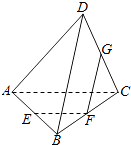
(1)求证:BD∥平面EFG;
(2)若AD=CD,AB=CB,求证:AC⊥BD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,对于
,对于 ![]() 上的任意x1 , x2 , 有如下条件:
上的任意x1 , x2 , 有如下条件:
① ![]() ;②|x1|>x2;③x1>|x2|;④
;②|x1|>x2;③x1>|x2|;④ ![]() .
.
其中能使g(x1)>g(x2)恒成立的条件序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设y=f(t)是某港口水的深度y(米)关于时间t(时)的函数,其中0≤t≤24.下表是该港口某一天从0时至24时记录的时间t与水深y的关系表:
t | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
y | 5 | 7.5 | 5 | 2.5 | 5 | 7.5 | 5 | 2.5 | 5 |
经长期观察,函数y=f(t)的图象可以近似地看成函数y=k+Asin(ωt+φ)的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com