
分析 (Ⅰ)利用函数f(x)=$\frac{ax+b}{x^2}$为奇函数,且f(1)=1,代入计算求实数a与b的值;
(Ⅱ)bn≥2017n恒成立,即:$\frac{{1-{q^2}}}{1-q}+\frac{{1-{q^3}}}{{1-{q^2}}}+…+\frac{{1-{q^{n+1}}}}{{1-{q^n}}}$≥2017n恒成立,分类讨论,即可求q的最小值.
解答 解:(Ⅰ)因为f(x)为奇函数,$\frac{-ax+b}{x^2}=-\frac{ax+b}{x^2}$,
得b=0,又f(1)=1,得a=1;
(Ⅱ)由$f(x)=\frac{1}{x}$,得$g(x)=\frac{x-1}{x^2}$,且$[g({a_n})•g({a_{n-1}})+\frac{{{a_n}+{a_{n-1}}-1}}{{{a_n}^2•{a_{n-1}}^2}}]•{a_n}^2=q$,
∴$\frac{a_n}{{{a_{n-1}}}}=q(n≥2)$∴${S_n}=\frac{{{a_1}(1-{q^n})}}{1-q}$,∴$\frac{{{S_{n+1}}}}{S_n}=\frac{{1-{q^{n+1}}}}{{1-{q^n}}}$.
由:${b_n}=\sum_{i=1}^n{\frac{{{S_{i+1}}}}{S_i}}=\frac{{1-{q^2}}}{1-q}+\frac{{1-{q^3}}}{{1-{q^2}}}+…+\frac{{1-{q^{n+1}}}}{{1-{q^n}}}$(q≥2016),
∵bn≥2017n恒成立,即:$\frac{{1-{q^2}}}{1-q}+\frac{{1-{q^3}}}{{1-{q^2}}}+…+\frac{{1-{q^{n+1}}}}{{1-{q^n}}}$≥2017n恒成立,
当q≥2016时,∵$\frac{{1-{q^{n+1}}}}{{1-{q^n}}}=\frac{{\frac{1}{q^n}-q}}{{\frac{1}{q^n}-1}}=\frac{q-1}{{1-\frac{1}{q^n}}}+1$,
再由复合函数单调性知,数列$\{\frac{{1-{q^{n+1}}}}{{1-{q^n}}}\}$为单调递减数列,
且n→∞时,$\frac{{1-{q^{n+1}}}}{{1-{q^n}}}=\frac{{\frac{1}{q^n}-q}}{{\frac{1}{q^n}-1}}→q$,
当q≥2017时,$\{\frac{{1-{q^{n+1}}}}{{1-{q^n}}}\}$中的每一项都大于2017,
∴$\frac{{1-{q^2}}}{1-q}+\frac{{1-{q^3}}}{{1-{q^2}}}+…+\frac{{1-{q^{n+1}}}}{{1-{q^n}}}$≥2017n恒成立;
当q∈[2016,2017)时,数列$\{\frac{{1-{q^{n+1}}}}{{1-{q^n}}}\}$为单调递减数列,
且n→∞时,$\frac{{1-{q^{n+1}}}}{{1-{q^n}}}=\frac{{\frac{1}{q^n}-q}}{{\frac{1}{q^n}-1}}→q$,而q<2017,
说明数列$\{\frac{{1-{q^{n+1}}}}{{1-{q^n}}}\}$在有限项后必定小于2017,设$\frac{{1-{q^{r+1}}}}{{1-{q^r}}}=2017+{M_r}(r=1,2,3,…,n)$,
且数列{Mn}也为单调递减数列,M1≥0.
根据以上分析:数列$\{\frac{{1-{q^{n+1}}}}{{1-{q^n}}}\}$中必有一项(设为第k项)$\frac{{1-{q^{k+1}}}}{{1-{q^k}}}=2017+{M_k}$,
(其中Mk≥0,且Mk+1<0)
∴$\frac{{1-{q^2}}}{1-q}+\frac{{1-{q^3}}}{{1-{q^2}}}+…+\frac{{1-{q^{n+1}}}}{{1-{q^n}}}=\frac{{1-{q^2}}}{1-q}+\frac{{1-{q^3}}}{{1-{q^2}}}+…+\frac{{1-{q^{k+1}}}}{{1-{q^k}}}+…+\frac{{1-{q^{n+1}}}}{{1-{q^n}}}$
=2017n+M1+M2+…+Mk+Mk+1+…+Mn(∵{Mn}为单调递减数列)
≤2017n+kM1+Mk+1+…+Mn≤2017n+kM1+(n-k)Mk+1,
当n→∞时,kM1+(n-k)Mk+1<0,∴$\frac{{1-{q^2}}}{1-q}+\frac{{1-{q^3}}}{{1-{q^2}}}+…+\frac{{1-{q^{n+1}}}}{{1-{q^n}}}<2017n$,
∴q∈[2016,2017)时,不满足条件.
综上所得:qmin=2017.
点评 本题考查函数的奇偶性,考查数列求和,考查分类讨论的数学思想,难度大.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | 函数f(x)的图象关于点(-$\frac{π}{6}$,0)对称 | |
| B. | 函数f(x)的图象关于直线x=-$\frac{π}{12}$对称 | |
| C. | 函数f(x)在区间[0,$\frac{5π}{12}$]上是增函数 | |
| D. | 函数f(x)的图象是由函数y=$\frac{1}{2}$sin2x的图象向右平移$\frac{π}{6}$个单位而得到 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{52}$ | B. | $\frac{1}{13}$ | C. | $\frac{1}{26}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
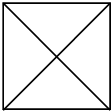 已知某几何体的俯视图是如图所示的正方形,正视图和侧视图都是底面边长为6,高为4的等腰三角形.
已知某几何体的俯视图是如图所示的正方形,正视图和侧视图都是底面边长为6,高为4的等腰三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (${\frac{1}{3}$,1) | B. | (${\frac{1}{2}$,1) | C. | (-${\frac{2}{3}$,1) | D. | ($\frac{2}{3}$,1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com