
【题目】已知t为实数,函数f(x)=2loga(2x+t﹣2),g(x)=logax,其中0<a<1.
(1)若函数y=g(ax+1)﹣kx是偶函数,求实数k的值;
(2)当x∈[1,4]时,f(x)的图象始终在g(x)的图象的下方,求t的取值范围;
(3)设t=4,当x∈[m,n]时,函数y=|f(x)|的值域为[0,2],若n﹣m的最小值为 ![]() ,求实数a的值.
,求实数a的值.
【答案】
(1)解:∵函数y=g(ax+1)﹣kx是偶函数,
∴loga(a﹣x+1)+kx=loga(ax+1)﹣kx,对任意x∈R恒成立,
∴2kx=loga(ax+1)﹣loga(a﹣x+1)=loga( ![]() )=x
)=x
∴k= ![]() ,
,
(2)解:由题意设h(x)=f(x)﹣g(x)=2loga(2x+t﹣2)﹣logax<0在x∈[1,4]恒成立,
∴2loga(2x+t﹣2)<logax,
∵0<a<1,x∈[1,4],
∴只需要2x+t﹣2> ![]() 恒成立,
恒成立,
即t>﹣2x+ ![]() +2恒成立,
+2恒成立,
∴t>(﹣2x+ ![]() +2)max,
+2)max,
令y=﹣2x+ ![]() +2=﹣2(
+2=﹣2( ![]() )2+
)2+ ![]() +2=﹣2(
+2=﹣2( ![]() ﹣
﹣ ![]() )2+
)2+ ![]() ,x∈[1,4],
,x∈[1,4],
∴(﹣2x+ ![]() +2)max=1,
+2)max=1,
∴t的取值范围是t>1,
(3)解:∵t=4,0<a<1,
∴函数y=|f(x)|=|2loga(2x+2)|在(﹣1,﹣ ![]() )上单调递减,在(﹣
)上单调递减,在(﹣ ![]() ,+∞)上单调递增,
,+∞)上单调递增,
∵当x∈[m,n]时,函数y=|f(x)|的值域为[0,2],且f(﹣ ![]() )=0,
)=0,
∴﹣1<m≤ ![]() ≤n(等号不同时取到),
≤n(等号不同时取到),
令|2loga(2x+2)|=2,得x= ![]() 或
或 ![]() ,
,
又[ ![]() ﹣(﹣
﹣(﹣ ![]() )]﹣[(﹣
)]﹣[(﹣ ![]() )﹣
)﹣ ![]() ]=
]= ![]() >0,
>0,
∴ ![]() ﹣(﹣
﹣(﹣ ![]() )>(﹣
)>(﹣ ![]() )﹣
)﹣ ![]() ,
,
∴n﹣m的最小值为(﹣ ![]() )﹣
)﹣ ![]() =
= ![]() ,
,
∴a= ![]() .
.
【解析】(1)根据偶函数的定义可得k的值;(2)构造函数h(x)=f(x)﹣g(x),根据对数函数的图象和性质可得,只需要t>﹣2x+ ![]() +2恒成立,根据二次函数的性质求出t的取值范围即可;(3)先判断函数y=|f(x)|的单调性,令|2loga(2x+2)|=2,得到x=
+2恒成立,根据二次函数的性质求出t的取值范围即可;(3)先判断函数y=|f(x)|的单调性,令|2loga(2x+2)|=2,得到x= ![]() 或
或 ![]() ,即可得到n﹣m的最小值为(﹣
,即可得到n﹣m的最小值为(﹣ ![]() )﹣
)﹣ ![]() =
= ![]() ,求出a即可.
,求出a即可.
【考点精析】根据题目的已知条件,利用函数单调性的判断方法的相关知识可以得到问题的答案,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=|ax﹣x2|+2b(a,b∈R).
(1)当a=﹣2,b=﹣ ![]() 时,解方程f(2x)=0;
时,解方程f(2x)=0;
(2)当b=0时,若不等式f(x)≤2x在x∈[0,2]上恒成立,求实数a的取值范围;
(3)若a为常数,且函数f(x)在区间[0,2]上存在零点,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x|x﹣a|+2x.
(1)若函数f(x)在R上是增函数,求实数a的取值范围;
(2)求所有的实数a,使得对任意x∈[1,2]时,函数f(x)的图象恒在函数g(x)=2x+1图象的下方;
(3)若存在a∈[﹣4,4],使得关于x的方程f(x)=tf(a)有三个不相等的实数根,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题
(1)已知函数f(x)=2x+ ![]() (x>0),证明函数f(x)在(0,
(x>0),证明函数f(x)在(0, ![]() )上单调递减,并写出函数f(x)的单调递增区间;
)上单调递减,并写出函数f(x)的单调递增区间;
(2)记函数g(x)=a|x|+2ax(a>1) ①若a=4,解关于x的方程g(x)=3;
②若x∈[﹣1,+∞),求函数g(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若将函数y=2sin2x的图象向左平移 ![]() 个单位长度,则平移后的图象的对称轴为( )
个单位长度,则平移后的图象的对称轴为( )
A.x= ![]() ﹣
﹣ ![]() (k∈Z)
(k∈Z)
B.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
C.x= ![]() ﹣
﹣ ![]() (k∈Z)
(k∈Z)
D.x= ![]() +
+ ![]() (k∈Z)
(k∈Z)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在高校自主招生中,某学校获得5个推荐名额,其中清华大学2名,北京大学2名,复旦大学1名.并且北京大学和清华大学都要求必须有男生参加.学校通过选拔定下3男2女共5个推荐对象,则不同的推荐方法共有( )
A.20种
B.22种
C.24种
D.36种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)=x2﹣2ax+5.
(1)若a>1,且函数f(x)的定义域和值域均为[1,a],求实数a的值;
(2)若不等式x|f(x)﹣x2|≤1对x∈[ ![]() ,
, ![]() ]恒成立,求实数a的取值范围.
]恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若y=f(x)=Asin(ωx+φ)(A>0,ω>0, ![]() 的部分图象如图所示.
的部分图象如图所示. 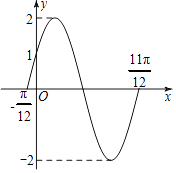
(I)求函数y=f(x)的解析式;
(II)将y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图象;若y=g(x)图象的一个对称中心为 ![]() ,求θ的最小值.
,求θ的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com