
【题目】在如图所示的棱长为1的正方体![]() 中,点P在侧面
中,点P在侧面![]() 所在的平面上运动,则下列命题中正确的( )
所在的平面上运动,则下列命题中正确的( )
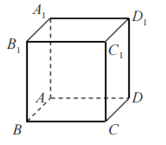
A.若点P总满足![]() ,则动点P的轨迹是一条直线
,则动点P的轨迹是一条直线
B.若点P到点A的距离为![]() ,则动点P的轨迹是一个周长为
,则动点P的轨迹是一个周长为![]() 的圆
的圆
C.若点P到直线AB的距离与到点C的距离之和为1,则动点P的轨迹是椭圆
D.若点P到直线AD与直线![]() 的距离相等,则动点P的轨迹是双曲线
的距离相等,则动点P的轨迹是双曲线
【答案】ABD
【解析】
A.根据![]() 平面
平面![]() ,判断点
,判断点![]() 的轨迹;B.根据平面与球相交的性质,判断选项;C.由条件可转化为
的轨迹;B.根据平面与球相交的性质,判断选项;C.由条件可转化为![]() ,根据椭圆的定义判断;D.由条件建立坐标系,求点
,根据椭圆的定义判断;D.由条件建立坐标系,求点![]() 的轨迹方程,判断轨迹是否是双曲线.
的轨迹方程,判断轨迹是否是双曲线.
A.在正方体![]() 中,
中,![]() 平面
平面![]() ,
,
所以![]() ,所以
,所以![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() ,
,
同理![]() ,所以
,所以![]() 平面
平面![]() ,
,
而点P在侧面![]() 所在的平面上运动,且
所在的平面上运动,且![]() ,
,
所以点![]() 的轨迹就是直线
的轨迹就是直线![]() ,故A正确;
,故A正确;
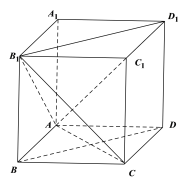
B.点![]() 的轨迹是以
的轨迹是以![]() 为球心,半径为
为球心,半径为![]() 的球面与平面
的球面与平面![]() 的交线,
的交线,
即点![]() 的轨迹为小圆,设小圆的半径为
的轨迹为小圆,设小圆的半径为![]() ,
,
球心![]() 到平面
到平面![]() 的距离为1,则
的距离为1,则![]() ,
,
所以小圆周长![]() ,故B正确;
,故B正确;
C. 点P到直线AB的距离就是点![]() 到点
到点![]() 的距离,
的距离,
即平面![]() 内的点
内的点![]() 满足
满足![]() ,
,
即满足条件的点![]() 的轨迹就是线段
的轨迹就是线段![]() ,不是椭圆,故C不正确;
,不是椭圆,故C不正确;
D.如图,过![]() 分别做
分别做![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,
,
则![]() 平面
平面![]() ,所以
,所以![]() ,过
,过![]() 做
做![]() ,连结
,连结![]() ,
,
![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() ,
,
如图建立平面直角坐标系,设![]() ,
,
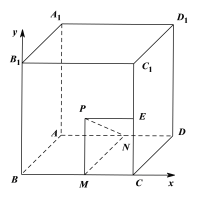
![]() ,则
,则![]() ,
,![]() ,
,
即![]() ,整理为:
,整理为:![]() ,
,
则动点![]() 的轨迹是双曲线,故D正确.
的轨迹是双曲线,故D正确.
故选:ABD


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
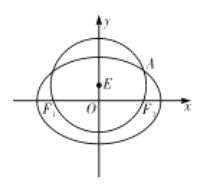
【题目】如图,已知圆![]() 经过椭圆
经过椭圆![]() 的左右焦点
的左右焦点![]() ,与椭圆
,与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() ,
, ![]() ,
, ![]() 三点共线.
三点共线.
(1)求椭圆![]() 的方程;
的方程;
(2)设与直线![]() (
(![]() 为原点)平行的直线交椭圆
为原点)平行的直线交椭圆![]() 于
于![]() 两点,当
两点,当![]() 的面积取取最大值时,求直线
的面积取取最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() 、
、![]() ,求
,求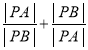 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆周率是圆的周长与直径的比值,一般用字母![]() 表示.我们可以通过设计一个试验来估计
表示.我们可以通过设计一个试验来估计![]() 的值:从
的值:从![]() 表示的区域内随机抽取200个实数对
表示的区域内随机抽取200个实数对![]() ,其中x,y两个数能与1构成钝角三角形三边长的数对
,其中x,y两个数能与1构成钝角三角形三边长的数对![]() 共有56个.则用随机模拟的方法估计
共有56个.则用随机模拟的方法估计![]() 的近似值为________.
的近似值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市居民用天然气实行阶梯价格制度,具体见下表:
阶梯 | 年用气量(立方米) | 价格(元/立方米) |
第一阶梯 | 不超过228的部分 | 3.25 |
第二阶梯 | 超过228而不超过348的部分 | 3.83 |
第三阶梯 | 超过348的部分 | 4.70 |
从该市随机抽取10户(一套住宅为一户)同一年的天然气使用情况,得到统计表如下:
居民用气编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年用气量(立方米) | 95 | 106 | 112 | 161 | 210 | 227 | 256 | 313 | 325 | 457 |
(1)求一户居民年用气费y(元)关于年用气量x(立方米)的函数关系式;
(2)现要在这10户家庭中任意抽取3户,求抽到的年用气量超过228立方米而不超过348立方米的用户数的分布列与数学期望;
(3)若以表中抽到的10户作为样本估计全市居民的年用气情况,现从全市中依次抽取10户,其中恰有k户年用气量不超过228立方米的概率为![]() ,求
,求![]() 取最大值时的值.
取最大值时的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
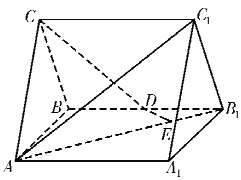
(I)若![]() 为
为![]() 上的一点,且
上的一点,且![]() 与直线
与直线![]() 垂直,求
垂直,求![]() 的值;
的值;
(Ⅱ)在(I)的条件下,设异面直线![]() 与
与![]() 所成的角为45°,求直线
所成的角为45°,求直线![]() 与平面
与平面![]() 成角的正弦值.
成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图为国家统计局网站发布的《2018年国民经济和社会发展统计公报》中居民消费价格月度涨跌幅度的折线图(注:同比是今年第![]() 个月与去年第
个月与去年第![]() 个月之比,环比是现在的统计周期和上一个统计周期之比)
个月之比,环比是现在的统计周期和上一个统计周期之比)
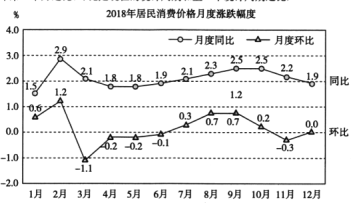
下列说法正确的是( )
①2018年6月CPI环比下降0.1%,同比上涨1.9%
②2018年3月CPI环比下降1.1%,同比上涨2.1%
③2018年2月CPI环比上涨0.6%,同比上涨1.4%
④2018年6月CPI同比涨幅比上月略微扩大1.9个百分点
A.①②B.③④C.①③D.②④.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com