
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
分析 本题通过对函数的定义域、值域、解析式的研究,从而判断选项中的函数是否为同一函数,不是同一函数的,只要列举一个原因即可.
解答 解:命题①,f(x)=x0,x≠0,g(x)=1中,x∈R,故不是同一个函数;
命题②,若f(x)=1,则f(x+1)=1,y=f(x),故y=f(x+1)有可能是同一个函数,该选项正确;
命题③,y=f(x)与y=f(t)解析式相同,定义域一致,y=f(x)与y=f(t)是同一个函数;
命题④,函数y=x与y=x+1,定义域和值域均为R,但由于对应法则不同,故浊相同的函数,选项④不正确.
故选B.
点评 本题考查了函数的表示、函数的定义域、值域、解析式,本题难度不大,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{6}{11}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
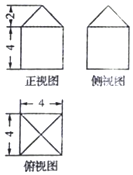
| A. | $80+16\sqrt{2}$ | B. | $96+13\sqrt{2}$ | C. | 96 | D. | 112 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
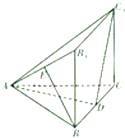 如图,几何体ABC-C1B1的底面ABC为等边三角形,侧面BB1C1C为矩形,B1B⊥平面ABC,E为边AB1的中点,D在边BC上移动.
如图,几何体ABC-C1B1的底面ABC为等边三角形,侧面BB1C1C为矩形,B1B⊥平面ABC,E为边AB1的中点,D在边BC上移动.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(λ)=$\frac{λ}{λ+2}$ | B. | f(λ)=$\frac{2λ}{λ+6}$ | C. | f(λ)=$\frac{3λ}{λ+7}$ | D. | f(λ)=$\frac{4λ}{λ+9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com