
【题目】已知函数![]() .
.
(1)求函数![]() 的单调递增区间;
的单调递增区间;
(2)在![]() 中,内角A,B,C所对的边分别为a,b,c,若
中,内角A,B,C所对的边分别为a,b,c,若![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)利用三角函数恒等变换的应用化简函数解析式可得f(x)=2sin(2x![]() ),利用正弦函数的单调性即可求解其单调递增区间.
),利用正弦函数的单调性即可求解其单调递增区间.
(2)由题意可得sin(2A![]() )=1,结合范围2A
)=1,结合范围2A![]() ∈(
∈(![]() ,
,![]() ),可求A的值,由正弦定理可得a,由余弦定理b,进而根据三角形的面积公式即可求解.
),可求A的值,由正弦定理可得a,由余弦定理b,进而根据三角形的面积公式即可求解.
(1)∵![]() sin2x﹣cos2x=2sin(2x
sin2x﹣cos2x=2sin(2x![]() ),
),
令2kπ![]() 2x
2x![]() 2kπ
2kπ![]() ,k∈Z,解得kπ
,k∈Z,解得kπ![]() x≤kπ
x≤kπ![]() ,k∈Z,
,k∈Z,
∴函数f(x)的单调递增区间为:[kπ![]() ,kπ
,kπ![]() ],k∈Z.
],k∈Z.
(2)∵f(A)=2sin(2A![]() )=2,
)=2,
∴sin(2A![]() )=1,
)=1,
∵A∈(0,π),2A![]() ∈(
∈(![]() ,
,![]() ),
),
∴2A![]() ,解得A
,解得A![]() ,
,
∵C![]() ,c=2,
,c=2,
∴由正弦定理![]() ,可得a
,可得a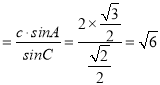 ,
,
∴由余弦定理a2=b2+c2﹣2bccosA,可得6=b2+4﹣2![]() ,解得b=1
,解得b=1![]() ,(负值舍去),
,(负值舍去),
∴S△ABC![]() absinC
absinC![]() (1
(1![]() )
)![]() .
.


科目:高中数学 来源: 题型:
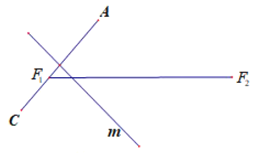
【题目】如图,已知平面内一动点![]() 到两个定点
到两个定点![]() 、
、![]() 的距离之和为
的距离之和为![]() ,线段
,线段![]() 的长为
的长为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 与轨迹
与轨迹![]() 交于
交于![]() 、
、![]() 两点,且点
两点,且点![]() 在线段
在线段![]() 的上方,线段
的上方,线段![]() 的垂直平分线为
的垂直平分线为![]() .
.
①求![]() 的面积的最大值;
的面积的最大值;
②轨迹![]() 上是否存在除
上是否存在除![]() 、
、![]() 外的两点
外的两点![]() 、
、![]() 关于直线
关于直线![]() 对称,请说明理由.
对称,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景区提供自行车出租,该景区有辆自行车供游客租赁使用,管理这些自行车的费用是每日![]() 元.根据经验,若每辆自行车的日租金不超过
元.根据经验,若每辆自行车的日租金不超过![]() 元,则自行车可以全部租出;若超出
元,则自行车可以全部租出;若超出![]() 元,则每超过
元,则每超过![]() 元,租不出的自行车就增加
元,租不出的自行车就增加![]() 辆.为了便于结算,每辆自行车的日租金
辆.为了便于结算,每辆自行车的日租金![]() (元)只取整数,并且要求租自行车一日的总收入必须高于这一日的管理费用,用
(元)只取整数,并且要求租自行车一日的总收入必须高于这一日的管理费用,用![]() (元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后得到的部分).
(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后得到的部分).
(1)求函数![]() 的解析式;
的解析式;
(2)试问当每辆自行车的日租金为多少元时,才能使一日的净收入最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
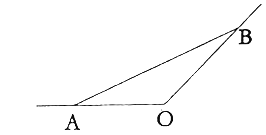
【题目】如图所示,某城市有一条从正西方AO通过市中心O后向东北OB的公路,现要修一条地铁L,在OA,OB上各设一站A,B,地铁在AB部分为直线段,现要求市中心O与AB的距离为![]() ,设地铁在AB部分的总长度为
,设地铁在AB部分的总长度为![]() .
.
![]() 按下列要求建立关系式:
按下列要求建立关系式:
![]() 设
设![]() ,将y表示成
,将y表示成![]() 的函数;
的函数;
![]() 设
设![]() ,
,![]() 用m,n表示y.
用m,n表示y.
![]() 把A,B两站分别设在公路上离中心O多远处,才能使AB最短?并求出最短距离.
把A,B两站分别设在公路上离中心O多远处,才能使AB最短?并求出最短距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com