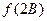已知函数
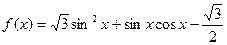
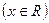
.
(1)若
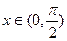
,求
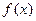
的最大值;
(2)在
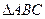
中,若
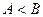
,

,求

的值
解:(1)
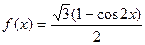
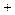
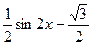
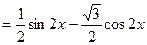
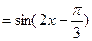
. 3分
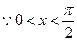
,
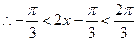
.
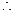
当
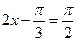
时,即
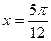
时,
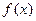
的最大值为
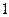
. 6分
(2)
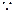
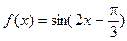
,
若
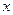
是三角形的内角,则
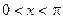
,
∴
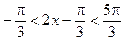
.
令
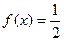
,得
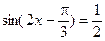
,
∴
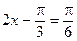
或
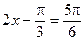
,
解得
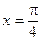
或

. 8分
由已知,
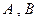
是△
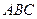
的内角,
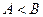
且
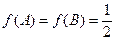
,
∴
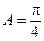
,
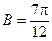
,

∴

. 10分
又由正弦定理,得
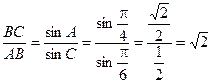
. 12分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
(本小题满分10分)
已知函数
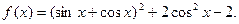
(1)求函数
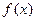
的最小正周期T;
(2)当

时,求函数
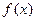
的最大值和最小值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题满分14分

)
已知向量
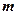
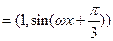
,
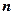
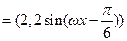
(其中
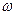
为正常数)
(Ⅰ)若
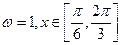
,求
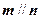
时
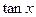
的值;
(Ⅱ)设
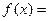
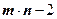
,若函数
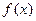
的图像的相邻两个对称中心的距离为
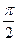
,求
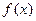
在区间
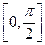
上的最小值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本题12分)
已知函数
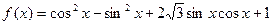
(1)求
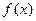
的最小正周期;
(2)若
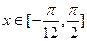
,求
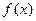
的最大值、最小值及相应的
x
的值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
(本小题满分10分)
已知向量
m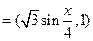
,
n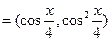
,函数
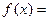 m
m·
n.
(Ⅰ)若
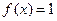
,求
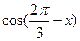
的值;
(Ⅱ)在锐角△ABC中,角A,B,C的对边分别是
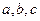
,且满足
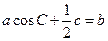
,求
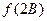
的取值范围。
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
.已知函数
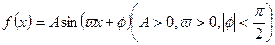
在一个周期内的部分函数图象如图所示.
(Ⅰ)求函数
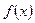
的解析式.
(Ⅱ)求函数
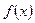
的单调递增区间.
(Ⅲ)求函数
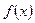
在区间
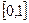
上的最大值和最小值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
函数
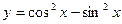
的周期是___________
查看答案和解析>>

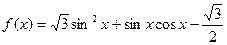
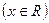 .
.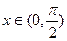 ,求
,求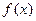 的最大值;
的最大值;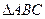 中,若
中,若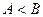 ,
, ,求
,求 的值
的值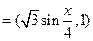 ,n
,n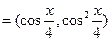 ,函数
,函数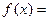 m·n.
m·n.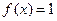 ,求
,求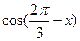 的值;
的值;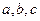 ,且满足
,且满足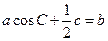 ,求
,求